Question

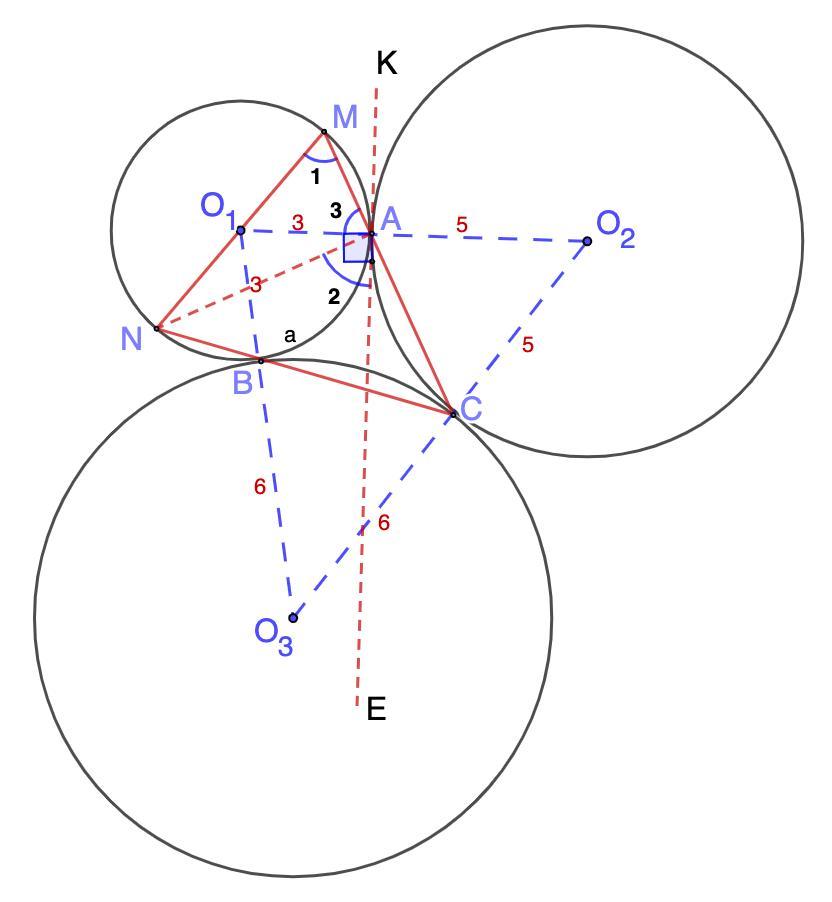
Первая окружность касается второй и третьей в различных точках A и B соответственно а вторая и третья касаются друг друга вточке C прямые AC и BC пересекают первую окружность в точках ответ M и N соответственно А) докажите что отрезок MN являются диаметром первой окружности
Б) радиусы первой, второй и третьей окружностей равны 3,5 и 6 соответственно Найдите площадь треугольника AMN​

Answer 1

Ответ:

1) Доказано, что MN - диаметр.

2) Площадь треугольника AMN равна $\displaystyle \bf \frac{27\sqrt{35} }{22}$ (ед².)

Объяснение:

Первая окружность касается второй и третьей в различных точках A и B соответственно, а вторая и третья касаются друг друга в точке C. Прямые AC и BC пересекают первую окружность в точках M и N соответственно.

А) докажите что отрезок MN являются диаметром первой окружности;

Б) радиусы первой, второй и третьей окружностей равны 3, 5 и 6 соответственно. Найдите площадь треугольника AMN.​

Дано: Окр.О₁, Окр.О₂, Окр.О₃.

А - точка касания Окр.О₁ и Окр.О₂;

В - точка касания Окр.О₁ и Окр.О₃;

С - точка касания Окр.О₂ и Окр.О₃;

АС ∩ Окр.О₁ = М; ВС ∩ Окр.О₁ = N;

O₁B = 3; O₂A = 5; O₃C = 6.

1) Доказать: MN - диаметр Окр.О₁;

2) Найти: S(AMN).

1) Доказательство.

1. Проведем касательную КЕ.

Обозначим ∠1, ∠2, ∠3 (см. рис.)

• Если две окружности касаются, то точка касания лежит на прямой, соединяющей их центры. Эта прямая перпендикулярна касательной, проведённой в точку касания окружностей.

⇒ ∠О₁АЕ = 90°

• Вписанный угол равен половине градусной меры дуги, на которую он опирается.

⇒    $\displaystyle \bf \angle1=\frac{1}{2} \smile AaN\;\;\;\;\;(1)$

• Угол между касательной и хордой равен половине градусной меры дуги, стягиваемой хордой.

⇒   $\displaystyle \bf \angle2=\frac{1}{2} \smile AaN\;\;\;\;\;(2)$

Из равенств (1) и (2) следует, что

∠1 = ∠2

2. Рассмотрим ΔMO₁A.

O₁M = O₁A  (радиусы одной окружности)

⇒ ΔMO₁A - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠1 = ∠3

3. ∠1 = ∠3 (п.2)

    ∠1 = ∠2 (п.1)

⇒ ∠2 = ∠3

∠О₁АЕ = ∠NAO₁ + ∠2 = 90°

⇒ ∠MAN = ∠NAO₁ + ∠3 = 90°

Прямой вписанный угол опирается на диаметр.

⇒ MN - диаметр.

2) Решение.

1. Рассмотрим ΔАО₁М и ΔАО₂С - равнобедренные.

• Вертикальные угла равны.

⇒ ∠3 = ∠САО₂

∠3 = ∠1 (п.2)

∠САО₂ = ∠О₂СА (углы при основании равнобедренного треугольника)

⇒ ∠3 = ∠1 = ∠САО₂ = ∠О₂СА

• Сумма уголов треугольника равна 180°.

⇒ ∠АО₁М = ∠АО₂С.

2. Рассмотрим ΔАО₁М и ΔО₁О₂О₃.

∠АО₁М = ∠АО₂С.

• Площади треугольников, имеющих равный угол, относятся как произведения сторон, содержащих этот угол.

  $\displaystyle \bf \frac{S(AO_1M)}{S(O_1O_2O_3)} =\frac{O_1M\cdot{O_1A}}{O_1O_2\cdot{O_2O_3}} =\frac{3\cdot3}{(3+5)(5+6)}=\frac{9}{88}\\\\S(AO_1M)=\frac{S(O_1O_2O_3)\cdot9}{88}$

Найдем площадь ΔО₁О₂О₃ по формуле Герона:

             $S=\sqrt{p(p-a)(p-b)(p-c)}$ ,

где р - полупериметр, а, b и с - стороны треугольника.

О₁О₂ = 3 + 5 = 8

О₂О₃ = 5 + 6 = 11

О₁О₃ = 3 + 6 = 9

р = (8 + 11 + 9) : 2 =14

$\displaystyle \bf S(O_1O_2O_3)=\sqrt{14(14-8)(14-11)(14-9)} =\sqrt{14\cdot6\cdot3\cdot5}=6\sqrt{35}$

$\displaystyle \bf S(AO_1M)=\frac{6\sqrt{35}\cdot9 }{88}=\frac{27\sqrt{35} }{44}$

3. Рассмотрим ΔAMN - прямоугольный.

АО₁ - медиана.

• Медиана делит треугольник на два равновеликих треугольника.

⇒

$\displaystyle \bf S(AMN)=2\cdot{S(AO_1M)}=\frac{27\sqrt{35} }{22}$ (ед².)

Площадь треугольника AMN равна $\displaystyle \bf \frac{27\sqrt{35} }{22}$ (ед².)

#SPJ1