У трикутнику ABC проведено бісектрису BK. На сторонах BA і BC позначили відповідно точки M і N такі, що ∠AKM = ∠CKN = ∠ABC. Доведіть, що пряма AC — дотична до кола, описаного навколо трикутника MBN.
siestarjoki:
неверное условие
должно быть AKM=CKN=ABС/2
Ответы
Ответ дал:
0
Дано: ∠AKM=∠CKN=∠ABC/2
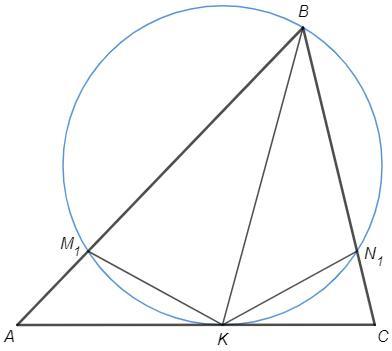
Построим окружность, которая касается AC в точке K и проходит через вершину B.
(центр - пересечение перпендикуляра к AC через K и серединного перпендикуляра к BK)
Пусть она пересекает сторону AB в точке M1.
∠AKM1 =∠ABK (угол между касательной и хордой)
От луча в полуплоскость можно отложить только один угол, равный данному.
Лучи KM и KM1 совпадают, точки M и M1 совпадают.
Аналогично точка N.
Пришли к условию задачи: AC касается окружности MBN.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад