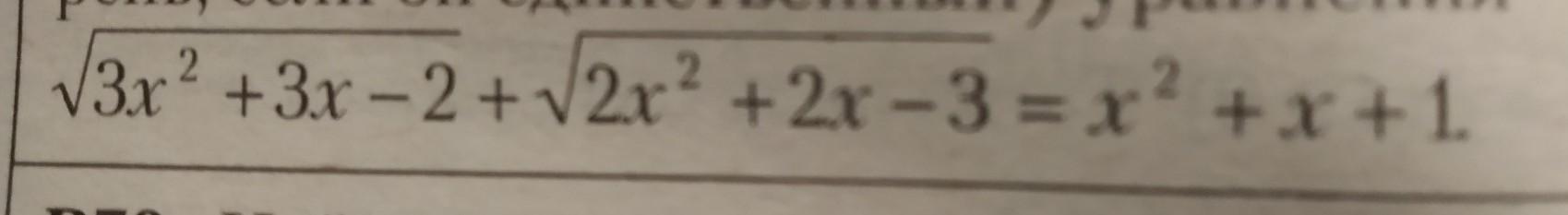Question

Помогите пожалуйста!!​

Answer 1

Ответ:

-3; -2; 1; 2

Пошаговое объяснение:

Пусть $\sqrt{3x^2+3x-2}=A,\sqrt{2x^2+2x-3}=B$. Рассмотрим выражение $A^2-B^2$: $A^2-B^2=3x^2+3x-2-2x^2-2x+3=x^2+x+1$ — это правая часть уравнения. Значит, уравнение имеет вид:

$A+B=A^2-B^2\\A+B=(A-B)(A+B)\\(A-B)(A+B)-(A+B)=0\\(A+B)(A-B-1)=0$

Рассмотрим случай A + B = 0:

$\sqrt{3x^2+3x-2}+\sqrt{2x^2+2x-3}=0$

Оба корня неотрицательны, значит, их равенство нулю возможно тогда и только тогда, когда оба они равны нулю:

$\displaystyle \left \{ {{\sqrt{3x^2+3x-2}=0,} \atop {\sqrt{2x^2+2x-3}=0}} \right. \left \{ {{x=\dfrac{-3\pm\sqrt{33}}{6},} \atop {x=\dfrac{-1\pm\sqrt{7}}{2}}} \right. \Rightarrow x\in\emptyset$

Система не имеет решений.

Рассмотрим случай A - B - 1 = 0:

$A=B+1\\\sqrt{3x^2+3x-2}=\sqrt{2x^2+2x-3}+1$

Обе части неотрицательны, возведём их в квадрат:

$3x^2+3x-2=2x^2+2x-3+2\sqrt{2x^2+2x-3}+1\\x^2+x=2\sqrt{2x^2+2x-3}$

Правая часть неотрицательна, значит, левая тоже должна быть неотрицательна:

$x^2+x\geq 0\Leftrightarrow x\in(-\infty;-1]\cup[0;+\infty)$

$x^4+2x^3+x^2=4(2x^2+2x-3)\\x^4+2x^3-7x^2-8x+12=0$

Сумма коэффициентов равна 0, значит, x = 1 является корнем уравнения:

$(x-1)(x^3+3x^2-4x-12)=0$

Среди делителей свободного члена (12) число x = 2 также является корнем уравнения:

$(x-1)(x-2)(x^2+5x+6)=0$

Оставшиеся корни по теореме Виета равны x = -3; -2.

Все корни удовлетворяют ограничению $x\in(-\infty;-1]\cup[0;+\infty)$.