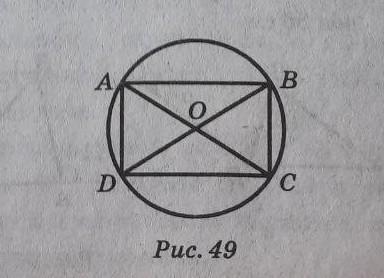
В окружности с центром О, проведены диаметры АС и BD (рис. 49). Докажите, что четырехугольник АВCD является прямоугольником. Найдите отрезок BD, если AD=7 см, угол ACD=30º.
Приложения:
brawlstarssssieieie:
помогите пожалуйста разобраться!:(
Удали эту задачу. Зачем тебе два одинаковых вопроса?
Все углы этого 4угольника вписаные и опираются на диаметр. Значит они прямые. Было бы очень странно, если бы 4угольник с 4 прямыми углами не оказался бы прямоугольником :)
Кстати, углы можно и тупо сосчитать. Скажем есть два равнобедренных треугольника (AOB и BOC, например), у которых углы при вершине дополняют друг друга до 180 градусов. Значит углы при основании в сумме (ну то есть угол OBA + угол OBC) будут 90. Это другой способ получить тот же результат.
Кажется, что я все очень понятно объяснил, но если попробовать записать это подробно, окажется, что я пропустил кучу строчек. Если вы восстановите их сами, то полностью разберетесь, как все устроено. В этой простенькой задачке.
Ответы
Ответ дал:
1
Відповідь:14=см.
Пояснення:
Розглянемо трикутник ADC. Так як ми знаємо що сума кутів трикутника дорівнює 180° то кут ACD дорівнює 30°, тоді кут АDC дорівнює 90°, звідси ми можемо знайти кут САD від 180 відняти 30 і відняти 90 і це буде 60 градусів. Тепер розглянемо трикутник АDО так як ми вже знаємо що кут CAD дорівнює 60°, а відрізки АО і OD радіуси кола то вони рівні, отже трикутник AOD рівносторонній, а в рівностороннього трикутника всі кути рівні. Отже ОD дорівнює АD. OD дорівнює ОВ бо вони радіуси кола. Отже ВD дорівнює ОВ додати OD і це дорівнює 7+7=14 см.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад