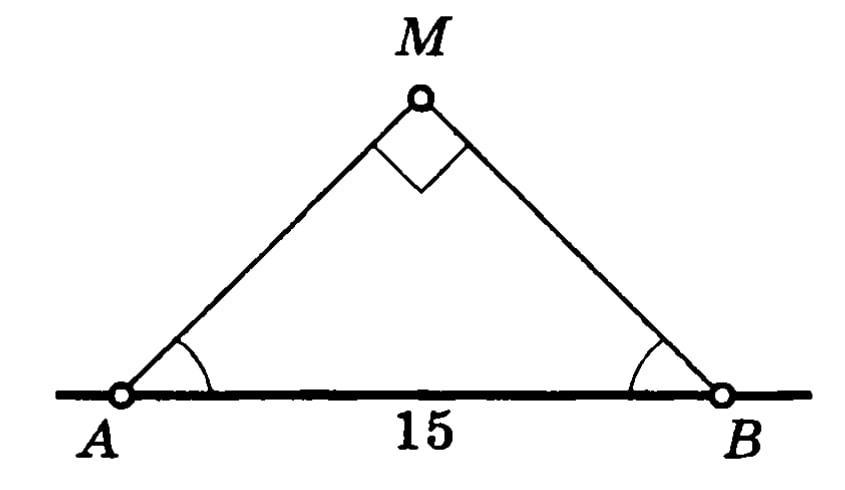
Ответы
Ответ:
7,5 см
Объяснение:
Δ АМВ - рівнобедрений (∠А=∠В= (180°-90°):2=45° - кути при основі АВ)
Проведемо перпендикуляр МС до прямої АВ.
т.я..Δ АМВ - рівнобедрений, то МС- висота, бісектриса та медіана⇒ АС=СВ=15:2=7,5 см
∠АМС=∠СМВ=∠АМВ:2=90°:2=45°
Розглянемо ΔАМС:
∠МАС=∠АМС=45°⇒ΔАМС - рівнобедрений з основою АМ⇒
АС=МС=7,5 см
Відповідь МС=7,5 см

Ответ:
7,5
Объяснение:
Так как ∠MAB = ∠MBA то ΔMBA равнобедренный. Также треугольник прямоугольный, то есть здесь можно применить теорему Пифагора. Пусть МА=х. Тогда MB также равен х, так как ΔMBA равнобедренный. Тогда проведем перпендикуляр MD, это и будет расстоянием от М до АВ. Также он будет высотой и медианой. По метрическим соотношениям h²= проекция α * проекция β. Так как МD - медиана , то AD=DB=7,5 , a AD и DB это проекции. То-есть MD= √(7,5*7,5)=7,5.