Ответы
Ответ дал:
2
Квадратная скобка означает союз "или" . Синус равен 1\2 , значит записываем два множества решений : или то , что записано в первой строчке , или то , что во второй . Откройте учебник и найдите тему "решение простейших тригонометрических уравнений" .
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
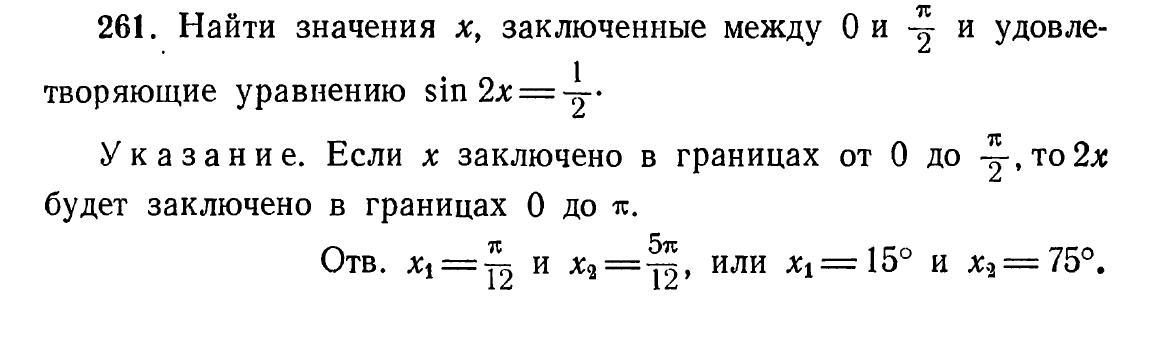
Особенно то что в квадратных скобках в самом начале. Откуда это взялось непонятно