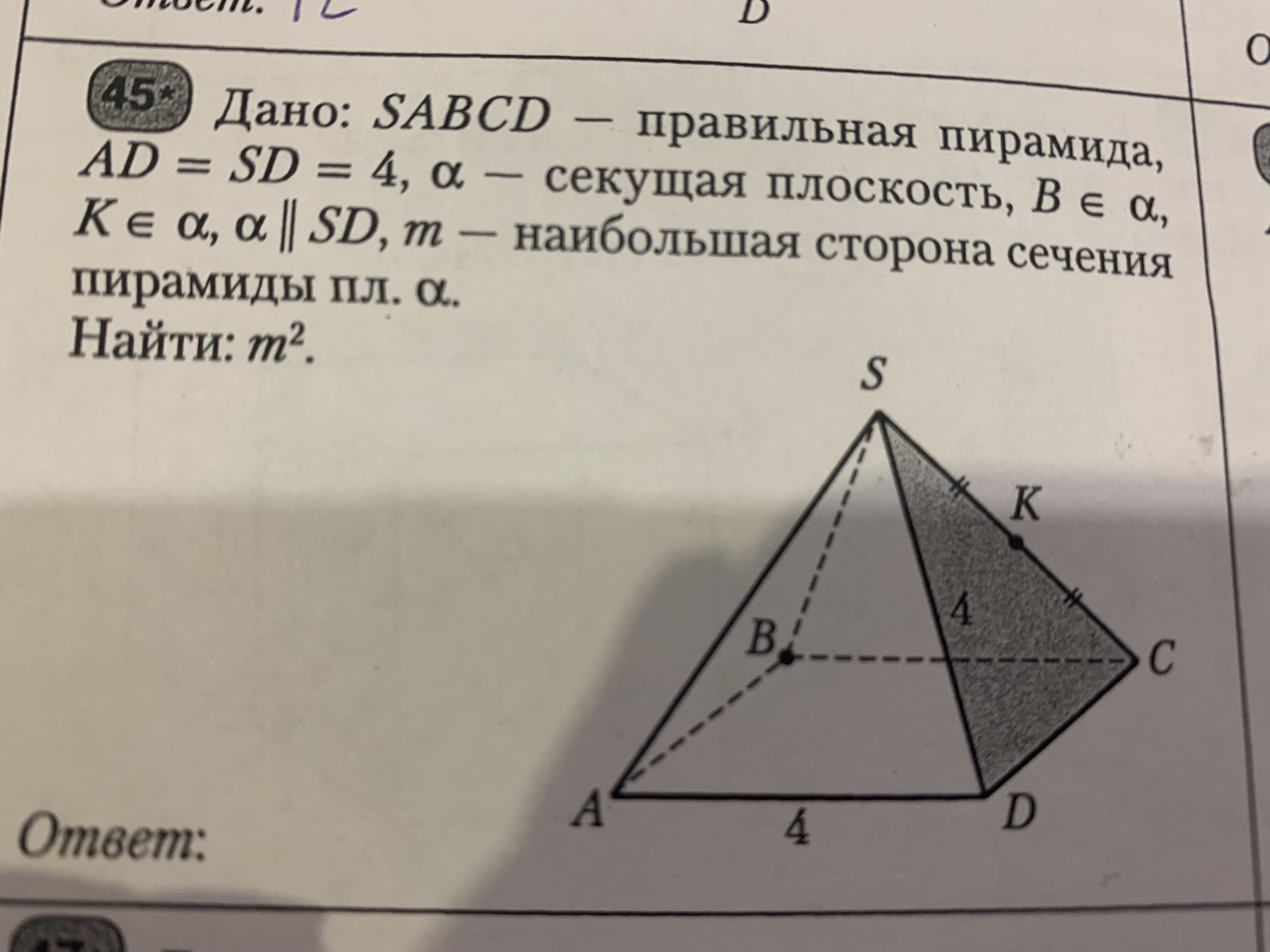
Дано: SABCD - правильная пирамида, AD=SD=4, a - секущая плоскость, В принадлежит а, К принадлежит а, a||SD, m - наибольшая сторона сечения пирамиды пл.a. Найти: m^2
Приложения:
Ответы
Ответ дал:
1
Ответ:
Объяснение: Проведем на грани SDC KР II SD , Р - находится на ребре DC.
Тогда КР - ср линия тр-ка SDC . КР= 1/2 SD= 2.
Искомое сечение - треугольник BKP.
KP= 2, так как тр-к KPC - равносторонний.
BSC- равносторонний ( по условию) => BK- высота =>
BK==
=
ABCD- квадрат ( по условию- пирамида правильная)
=> BP>BK>KP
=> m= BP =>
Вас заинтересует
2 года назад
2 года назад
7 лет назад