Две окружности имеют общий центр. Прямая пересекает обе окружности. Докажите, что отрезки этой прямой, заключённые между окружностями равны
Ответы
Ответ дал:
1
Ответ:
Объяснение:
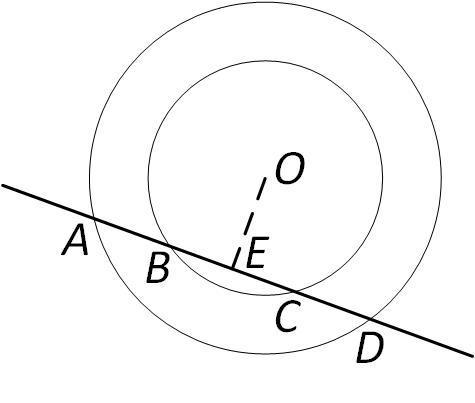
Рассмотрим две концентрические окружности и секущую, которая пересекает бо́льшую окружность в точках и
а меньшую — в точках
и
Из центра окружностей точки
опустим перпендикуляр
на секущую. Так как треугольники
и
равнобедренные, точка
в каждом из них является еще и основанием медианы, т. е.
и
Тогда и отрезки
и
равны.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад