Бісектриса AL прямокутника ABCD , периметр якого дорівнює 64 см, ділить його
сторону у відношенні 3 : 2 рахуючи від вершини В. Знайдіть довжину більшої сторони
прямокутника.
Ответы
Ответ:
Длина большей стороны прямоугольника равна 20 см.
Пошаговое объяснение:
Биссектриса AL прямоугольника ABCD , периметр которого равен 64 см, делит его сторону в отношении 3 : 2 считая от вершины В. Найдите длину большей стороны прямоугольника.
Дано: ABCD - прямоугольник;
AL - биссектриса;
Р(ABCD) = 64 см;
BL : LC = 3 : 2
Найти: ВС.
Решение:
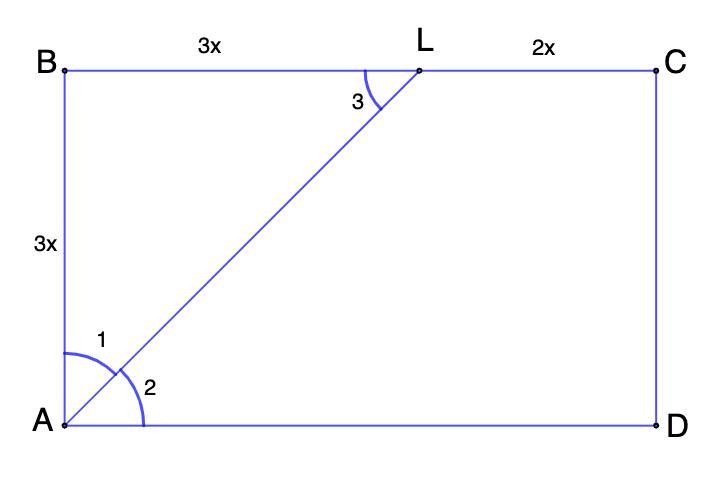
Обозначим углы 1, 2, 3. (см. рис)
1. Рассмотрим ΔABL.
∠1 = ∠2 (AL - биссектриса)
∠3 = ∠2 (накрест лежащие при BC || AD и секущей AL)
⇒ ∠1 = ∠3
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ АВ = ВL.
2. BL : LC = 3 : 2 (условие)
Пусть BL = 3x см, тогда LC = 2x см, а ВС = 5х см.
⇒ АВ = ВL = 3x см.
- Периметр прямоугольника равен удвоенной сумме смежных сторон.
Р(ABCD) = 2(AB + BC)
64 = 2(3x + 5x)
8x = 32 |:8
x = 4
⇒ AB = 3x = 12 см
ВС = 5х = 20 см
Длина большей стороны прямоугольника равна 20 см.
Доброї, спокійної ночі.
Відповідь: 20 см.
Покрокове пояснення: фото
