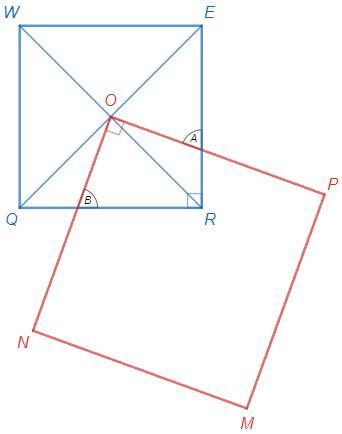
На плоскости расположены два квадрата, `QWER` и `MNOP`. Известно, что `QW = 40`, `MN = 50`, точка `О` – центр квадрата `QWER`, а отрезки `OP` и `RE` пересекаются под углом {70}. Найдите площадь общей части двух квадратов
Ответы
Ответ дал:
0
OARB - вписанный (противоположные углы 90°)
∠A=∠B (внешний угол вписанного четырехугольника равен противолежащему внутреннему)
∠OEA=∠ORB=45° (диагонали квадрата являются биссектрисами)
OE=OR (диагонали квадрата равны и точкой пересечения делятся пополам)
В треугольниках AOE и BOR два угла равны, следовательно все углы равны. Треугольники равны по стороне и прилежащим углам. Их площади равны. Тогда площадь OARB равна площади ROE, то есть четверти площади QWER, 400.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад