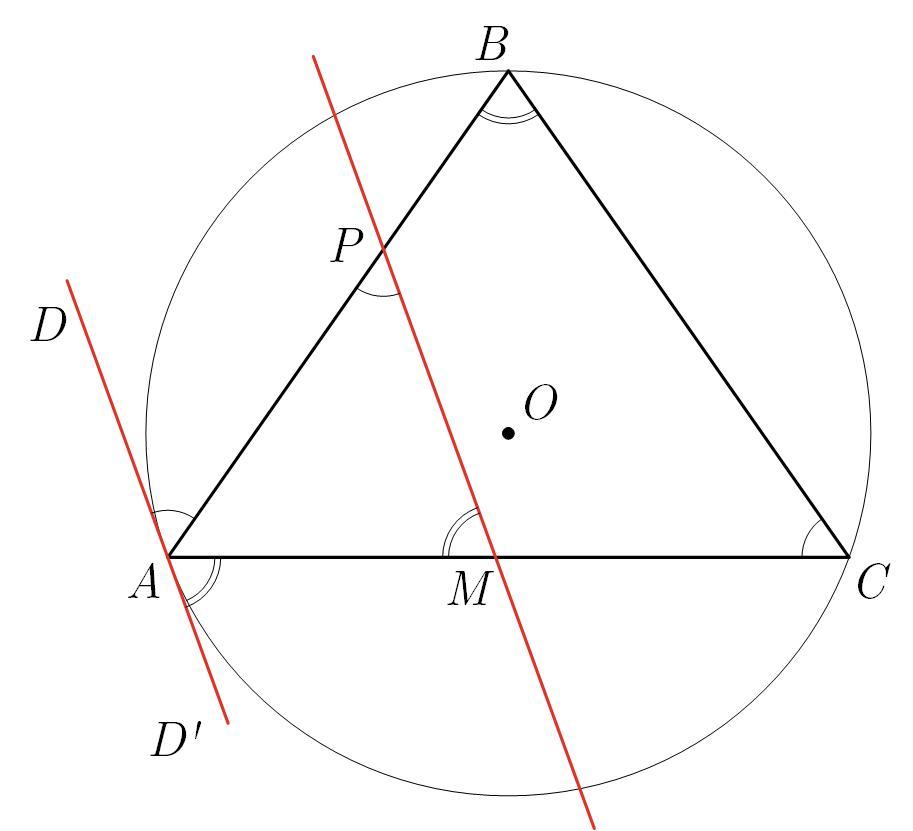
Пряма AD— дотична до описаного кола трикутника АВС. Пряма, паралельна цій дотичній, перетинає сторони AB i AC у точках р і М відповідно. Відомо, що кути АСВ i ABC дорівнюють відповідно 55° і 70°. Знайдіть кути трикутника АМР.
antonovm:
так он (АМР) подобен АВС ( используйте равенство накрест лежащих и также тот факт , что угол межу касательной и хордой равен вписанному углу , опирающемуся на эту хорду )
Ответы
Ответ дал:
3
Ответ:
Объяснение:
Так как прямые и
параллельны, а
и
секущие,
,
.
Но по теореме о касательной и хорде угол между касательной и хордой равен половине дуги, которую эта хорда стягивает, т. е. равен вписанному углу, опирающемуся на эту хорду.
Поэтому ,
.
Значит углы треугольника точно такие же, как и у треугольника
:
,
,
.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад