Ответы
Ответ дал:
0
Ответ:
Высота трапеции равна
Объяснение:
Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
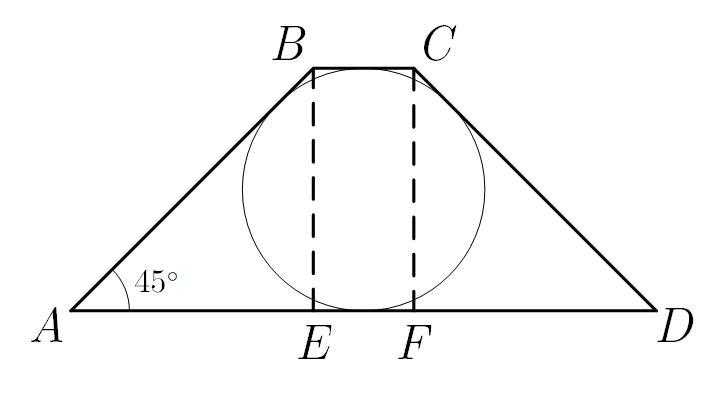
Опустим из вершин и
высоты
и
на нижнее основание. Тогда прямоугольные треугольники
и
— равнобедренные,
.
Из прямоугольного треугольника по теореме Пифагора
Значит сумма противоположных боковых сторон трапеции равна и равна сумме оснований.
Тогда длина средней линии трапеции равна
По формуле площади трапеции
откуда ,
.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
