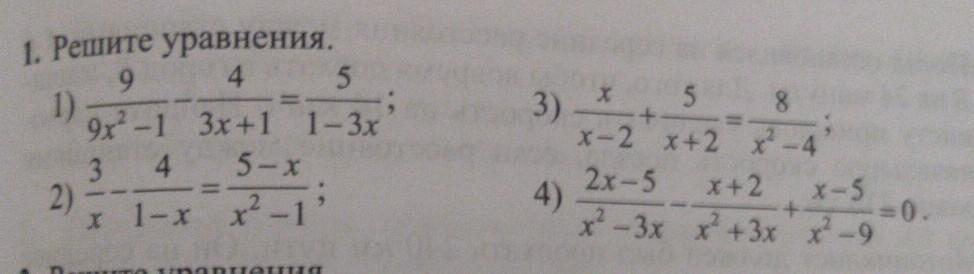Ответы
Ответ дал:
2
Первое
ОДЗ:
Помня про ОДЗ, умножим обе части на (3x-1)(3x+1):
Второе
ОДЗ: ,
Помня про ОДЗ, умножим обе части уравнения на знаменатель:
Третье
ОДЗ:
Помня про ОДЗ, умножим обе части уравнения на знаменатель:
Первый икс не подходит по ОДЗ.
Ответ:
Четвёртое
ОДЗ: ,
Помня про ОДЗ, избавимся от знаменателя:
Первый корень не подходит по ОДЗ.
Ответ:
Если что-нибудь непонятно — спрашивай.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад