У трикутник зі стороною 10 см і висотою 7 см, проведеною, до даної
сторони, вписано прямокутник, сторони якого відносяться як 4:7,
причому менша сторона прямокутника належить даній стороні
трикутника. Знайдіть сторони прямокутника.
Ответы
Ответ дал:
0
Ответ:
Стороны прямоугольника равны 5 и
Объяснение:
Пусть ;
,
.
Так как , то
.
Треугольники и
подобны, поэтому
Тогда
Приложения:
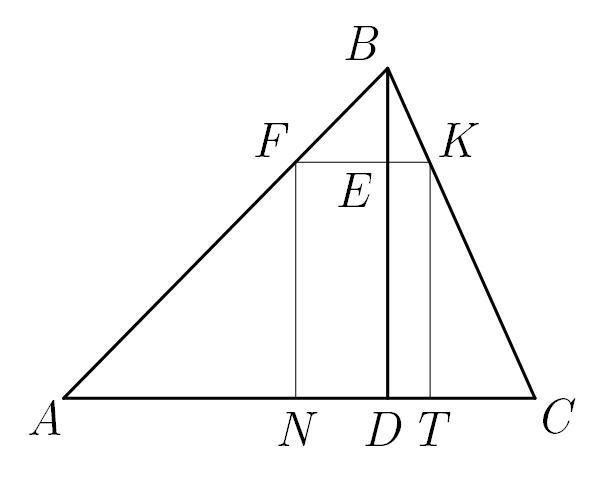
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад