З точки поза колом проведено дотичну, довжина якої дорівнює 12 см.
Обчисліть радіус кола, якщо відстань від цієї точки до кола дорівнює 9
см.
Ответы
Ответ дал:
0
Ответ:
Объяснение:
З'єднаємо крапку з центром кола. Тоді відрізок від точки до точки перетину кола є відстань до кола. Проведемо радіус до точки дотику, звідси маємо прямокутний трикутник, у якому катети - це дотична (12 см) і радіус R, а гіпотенуза - відстань від точки дотику до кола (9 cм) + радіус R.
За теоремою Піфагора маємо:
12² + R²= (9 + R)²
144 + R²= 81 + 18R + R²
18R = 63
R = 63 : 18
R = 3,5 см радіус кола
Приложения:
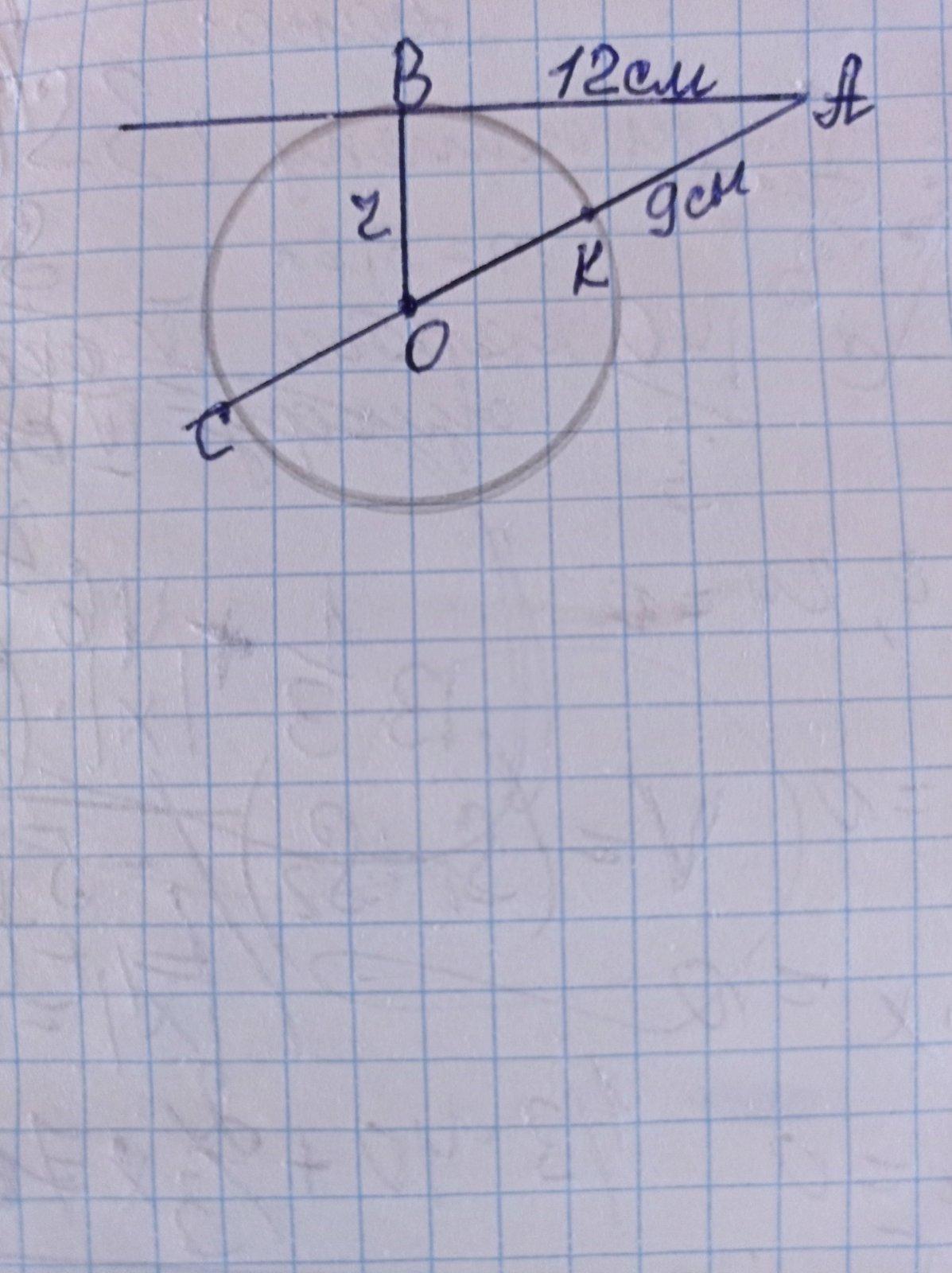
cos20093:
Пусть AO=d; (d+R)(d-R)=12²; d-R=9; => d+R=12²/9=16; R=(16-9)/2=7/2; так считать немного проще. Кто знаком с определением степени точки относительно окружности, сразу все узнАет.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад