Question

Сторона основания правильной четырехугольной пирамиды равна 8 см, а ее
объем равен 256 см3. Какова высота этой пирамиды? Какова площадь полной поверхности этой пирамиды?

Answer 1

Ответ:

Высота пирамиды равна 12см, площадь полной поверхности

64( √10+1) см².

Объяснение:

Сторона основания правильной четырехугольной пирамиды равна 8 см, а её объем 256 см ³. Какова высота пирамиды? Какова площадь полной поверхности пирамиды?

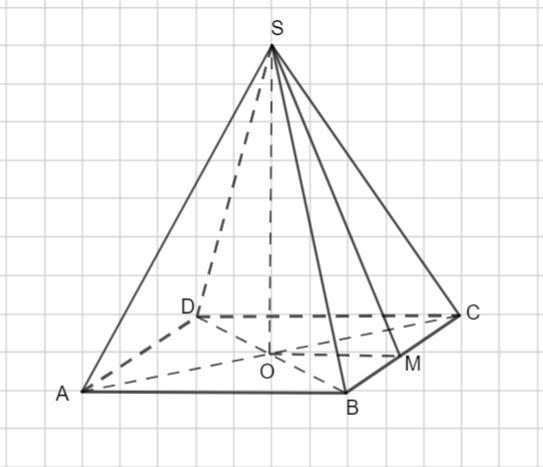
Рассмотрим SABCD - правильную четырехугольную пирамиду. Тогда в основании пирамиды - квадрат ABCD

Площадь квадрата определяется по формуле

$S =a^{2} , a-$ сторона квадрата.

По условию а = 8 см.

Тогда площадь основания будет равна

$S =8^{2} =8\cdot8 =64$ cм²

По условию задан объем пирамиды. Объем пирамиды определяется по формуле

$V =\dfrac{1}{3} S\cdot H$

$256 =\dfrac{1}{3} \cdot 64\cdot H;\\\\H =\dfrac{3\cdot256}{64} =3\cdot 4 =12$

Значит, высота пирамиды равна 12 см.

Площадь полной поверхности пирамиды равна сумме площади основания и площади боковой поверхности пирамиды.

Площадь боковой поверхности пирамиды равна полупроизведению периметра основания на апофему.

SM - апофема ( высота боковой грани правильной пирамиды)

SO=H= 12 см.

ОМ = а :2=8: 2 =4 см.

Рассмотрим Δ SOМ - прямоугольный и найдем SМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$SM ^{2} =SO^{2} +OM^{2} ;\\SM =\sqrt{SO^{2} +OM^{2}} ;\\SM =\sqrt{12^{2} +4^{2} } =\sqrt{144+16} =\sqrt{160} =\sqrt{16\cdot10} =4\sqrt{10}$ см.

Периметр квадрата определяется по формуле :

Р=4а

$P= 4\cdot 8 =32$ см.

Тогда площадь боковой поверхности будет

$S =\dfrac{1}{2} \cdot 32 \cdot 4 \sqrt{10} =16\cdot 4 \sqrt{10} =64 \sqrt{10}$ см².

А площадь полной поверхности

$S =64\sqrt{10} +64=64( \sqrt{10} +1)$  см²