Question

Две бригады могут проделать всю работу, работая вместе, за 18 дней. Если
первая бригада будет работать сама 9 дней, а впоследствии приступит к работе вторая, то
для окончания работы им нужно еще 12 дней. За сколько дней выполнит работу первая
бригада, работая самостоятельно?

Answer 1

Пусть производительность первой бригады равна $v_1$, а второй — $v_2$. Примем всю работу за единицу:

$\begin{cases}v_1+v_2=\dfrac{1}{18}\\9v_1+12(v_1+v_2)=1\end{cases}\\\begin{cases}18v_1+18v_2=1\\9v_1+12v_1+12v_2=1\end{cases}\\\begin{cases}18v_1+18v_2=1 \\ 21v_1+12v_2=1\end{cases}\\\begin{cases}-36v_1-36v_2=-2\\63v_1+36v_2=3\end{cases}$

Сложим оба уравнения:

$27v_1=1\\v_1=\dfrac{1}{27}$

За день бригада выполняет 1/27 работы, а значит, всю работу выполнит за 27 дней.

Ответ: за 27 дней.

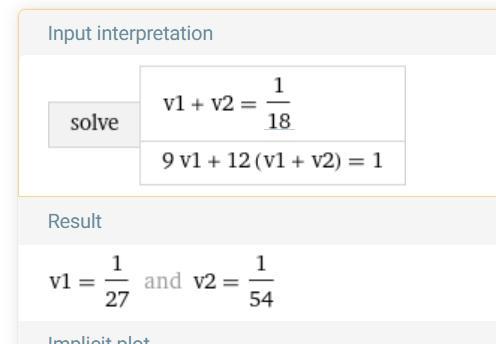
На скриншоте проверка на компьютере.

Если что-нибудь непонятно — спрашивай.