В треугольнике ABC на стороне AC отмечена точка К так, что AK=AB. Угол ABK = 75°. Угол АВС = 60°. Найти АС, если известно, что ВС = 3
Пеппер:
проверьте условие
Проверил, там так и написано, я не понимаю, опечатка это или так задумано
Ответы
Ответ дал:
2
Ответ:
Объяснение:
Так как , точка
не может быть внутренней точкой отрезка
, а может принадлежать прямой
.
Находиться на продолжении стороны за точку она не может, иначе из равенства углов
и
следует, что в треугольнике
Значит точка находится на продолжении стороны
за точку
.
В прямоугольном треугольнике
значит
#SPJ1
Приложения:
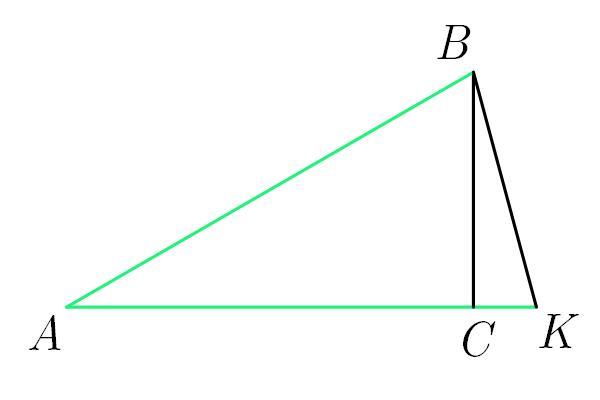
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад