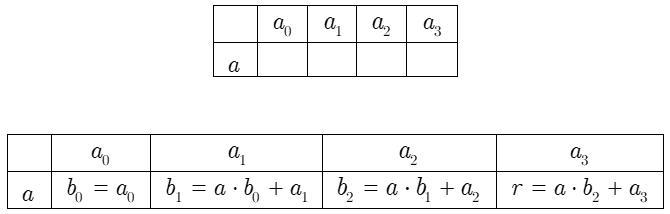Question

Решить по схеме Горнера
3x³ +5x² +5x+3=0;
x³+3x²-16x-48=0;
x⁴-3x³+x-3=0.​

Answer 1

Ответ:

$1)\ -1;\ 2)\ -3,\ \pm 4;\ 3)\ 3$

Объяснение:

Если приведенный (старший коэффициент равен 1) многочлен $P(x)$ с целочисленными коэффициентами имеет целые корни, то они являются делителями свободного члена.

Если неприведенный (старший коэффициент не равен 1) многочлен $P(x)$ с целочисленными коэффициентами имеет рациональные корни, то они являются несократимыми дробями, в которых числитель является делителем свободного члена, а знаменатель — делителем старшего коэффициента.

Схема Горнера позволяет легко установить остаток от деления и коэффициенты частного от деления многочлена $P(x)$ на бином $x - a.$ В случае, если $x = a$ является корнем этого многочлена, остаток будет равен 0.

Для примера, кубический многочлен $P(x) = {a_0}{x^3} + {a_1}{x^2} + {a_2}x + {a_3},$ двучлен $x - a.$

Составляем таблицу (см. рис), правило заполнения которой см. на рис. ниже.

Это эквивалентно такой записи:

${a_0}{x^3} + {a_1}{x^2} + {a_2}x + {a_3} = (x - a)({b_0}{x^2} + {b_1}x + {b_2}) + r.$

1) $3{x^3} + 5{x^2} + 5x + 3 = 0.$

Ищем рациональный корень этого уравнения среди чисел  $\pm \displaystyle\frac{1}{3},\,\, \pm 1,\,\, \pm 3.$

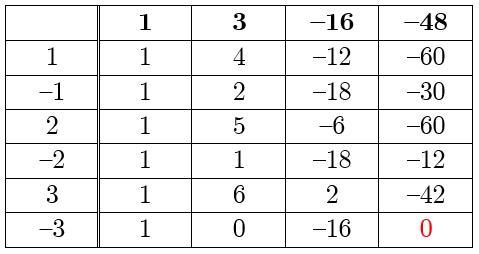
Схема Горнера — см. рис.

Так как все коэффициенты многочлена положительны, понятно, что корень может быть только отрицательный.

Квадратное уравнение $3{x^2} + 2x + 3 = 0$ корней не имеет, т. к. его дискриминант $D = {2^2} - 4 \cdot 3 \cdot 3 < 0.$

Таким образом, данное уравнение имеет корень $x = - 1.$

2) ${x^3} + 3{x^2} - 16x - 48 = 0.$

Ищем целый корень этого уравнения среди чисел  $\pm 1,\,\, \pm 2,\,\, \pm 3,\,\, \pm 4,\,\, \pm 6,\,\, \pm 8,\,\, \pm 12,\,\, \pm 16,\,\, \pm 24,\,\, \pm 48.$

Схема Горнера — см. рис.

Квадратное уравнение ${x^2} - 16 = 0$ имеет еще два корня: $x = \pm 4.$

Таким образом, данное уравнение имеет корни $x = - 3,\ x = \pm 4.$

3) ${x^4} - 3{x^3} + x - 3 = 0.$

Ищем целый корень этого уравнения среди чисел  $\pm 1,\,\, \pm 3.$

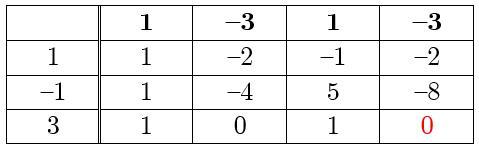
Схема Горнера — см. рис.

Квадратное уравнение ${x^2} + 1 = 0$ корней не имеет.

Таким образом, данное уравнение имеет корень $x = 3.$