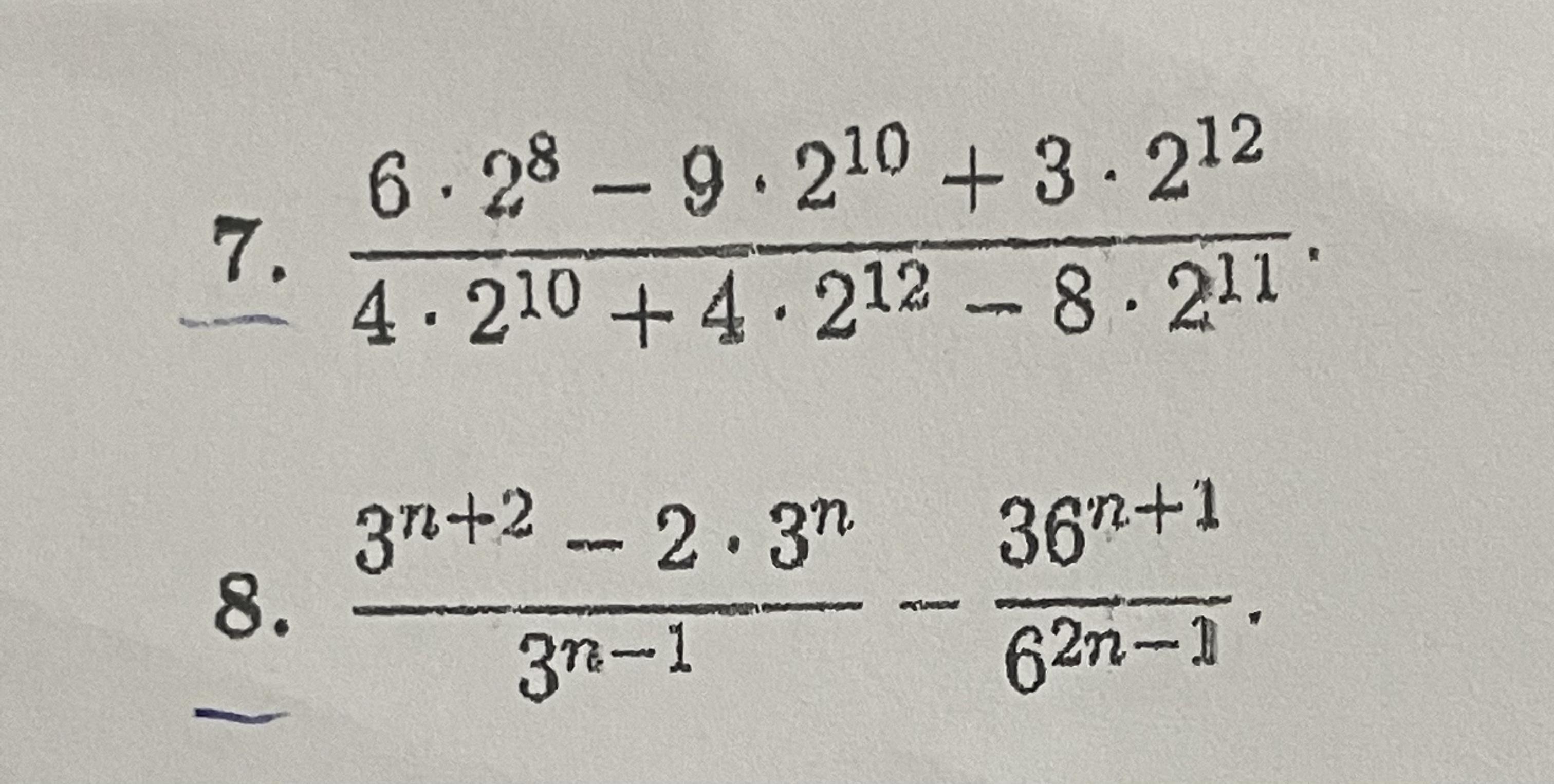Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Воспользуемся свойствами степеней:
:
TylerYago:
Не понимаю почему 1,0, это же правильно
Конкуренты :) Есть такие мелкие людишки, которые пока никто не видит то коврик описают, то дверь мелом изрисуют...
Для ТуlerYago. Якщо ви про зірки, то я вам поясню. Оскільки ви тут нещодавно, то мабуть не знаєте де-яких нюансів. Не всі працюють з компа. Більшість зі смартфонів. І коли гортають сторінку, випадково попадають на зірку. І це може бути і одна, і дві при абсолютно правильній відповіді, і навпаки всі 5 при невірній відповіді. Іноді автор питання думає , що прапорець порушення це подяка. І таке буває.
Спасибо :) Мне, честно сказать, не очень важно, сколько там звезд — это же не коньяк :) Я не знаю, на что они в конечном счете влияют, но точно не на мою самооценку.
Ні на що, це для дітей. Як ті смішні "досягнення": розумний, дуже розумний, професор. Добре , що не професор Кембриджу.
Ответ дал:
1
Розв'язання завдання додаю.
7. 1,125, 8. -195
Приложения:
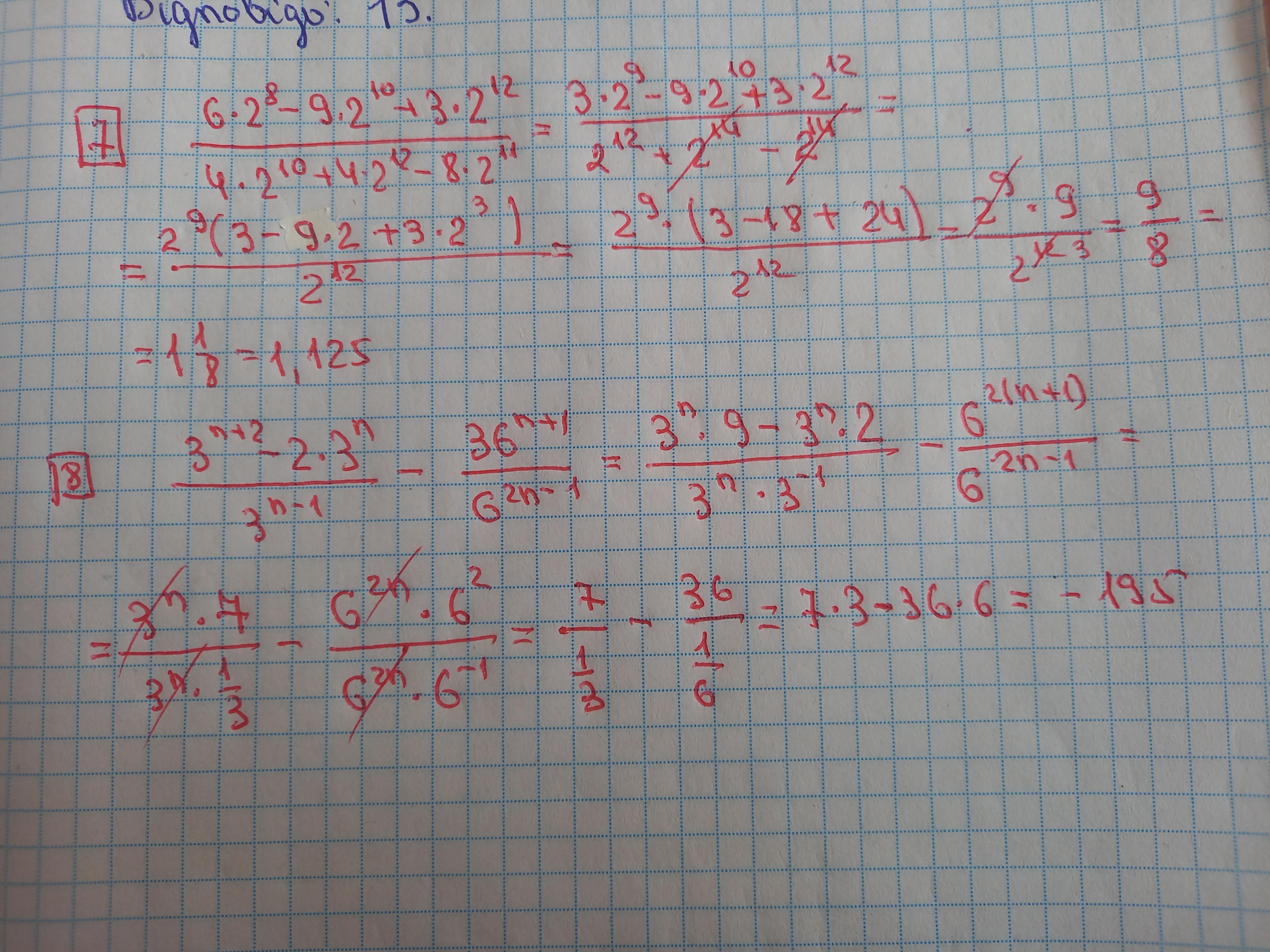
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад