Question

Решить как в геом. задачках

Answer 1

Ответ:

на фото

Объяснение:

Answer 2

Ответ:

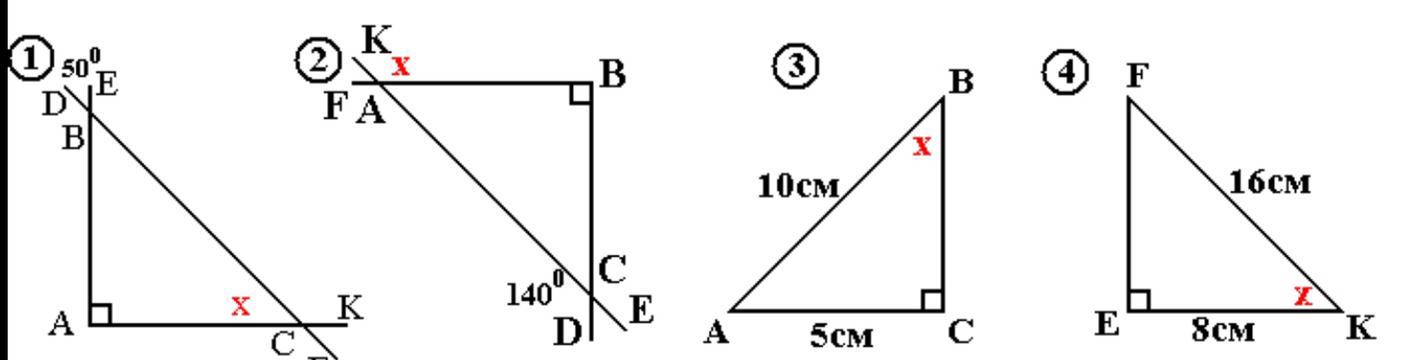
1)∠ACB=40°

2)∠KAB=130°

3)∠АВС=30°

4)∠FKE=60°

Объяснение:

1) ∠DBE=50°, ∠BAC=90°.

∠DBE=50°, ∠BAC=90°.∠ACB-?

∠ABC=∠DBE=50° - как вертикальные.

• Сумма острых углов прямоугольного треугольника равна 90°.

Поэтому ∠ACB=90°-∠ABC=90°-50°=40°.

2)∠ACD=140°, ∠ABC=90°,

∠ACD=140°, ∠ABC=90°, ∠KAB-?

Так как ∠ACD и ∠ACB - смежные, то их сумма равна 180°.

Значит ∠ACB=180°-∠ACD=180°-140°=40°.

∠KAB является внешним углом треугольника АВС.

• Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.

Следовательно ∠KAB=∠ABC+∠ACB=90°+40°=130°.

3)AB=10см, AC=5см, ∠С=90°.

AB=10см, AC=5см, ∠С=90°.∠ABC-?

Видим, что катет AC равен половине гипотенузы АВ:

AC=½•AB

5=½•10

Известно, что:

• Катет прямоугольного треугольника, равный половине гипотенузы, лежит напротив угла в 30° .

Следовательно ∠АВС=30°.

4) FК= 16см, EK=8см, ∠Е=90°.

FК= 16см, EK=8см, ∠Е=90°.∠FKE-?

Опять замечаем, что катет EK=½•FK:

8=½•16

Следовательно ∠EFK=30°.

Сумма острых углов прямоугольного треугольника равна 90°, значит:

∠FKE=90°-∠EFK=90°-30°=60°.