Question

помогите! очень срочно ​

Answer 1

Ответ:

Высота пирамиды равна 12 ед.

Объяснение:

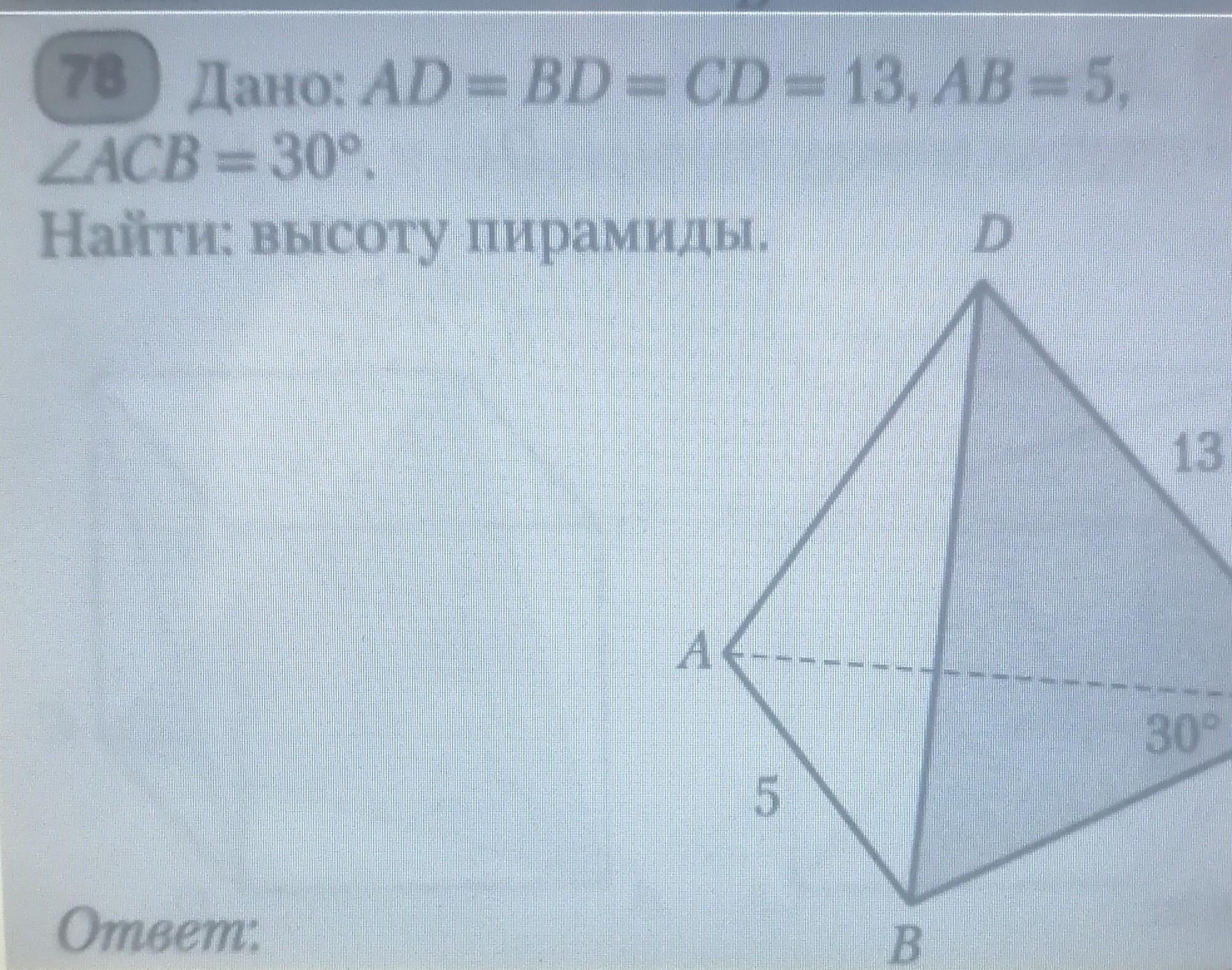
Дано: AD=BD=CD =13 ,

AB =5, ∠ACB =30°.

Найти: высоту пирамиды

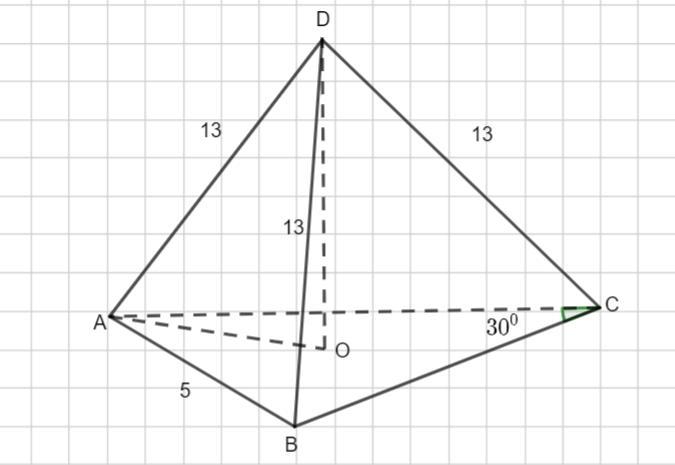
Пусть дана пирамида DАВС , DО -высота. AD=BD=CD =13

Так как  все  боковые ребра равны, то вершина пирамиды проектируется в центр описанной окружности. Точка О -центр описанной окружности около  ΔАВС.

Тогда АО  - радиус окружности, описанной около ΔАВС.

Радиус окружности, описанной около треугольника определяется по формуле

$R =\dfrac{a}{2sin\alpha } ,$

где а -сторона треугольника, α - противолежащий угол.

Тогда

$R =\dfrac{AB }{2sinACB } ;\\\\R =\dfrac{5}{2sin30^{0} } =\dfrac{5}{2\cdot0,5} =\dfrac{5}{1} =5$

Значит, АО =5 ед.

Рассмотрим ΔАОD- прямоугольный. Найдем высоту пирамиды по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AD^{2} =AO^{2} +OD^{2} ;\\OD^{2} =AD^{2} -AO^{2};\\OD =\sqrt{13^{2} -5^{2} } =\sqrt{169-25} =\sqrt{144} =12$

Высота пирамиды равна 12 ед.