Ответы
Ответ дал:
0
Ответ:
Объяснение:
При логарифм убывающая функция, а при
— возрастающая. С учетом этого получаем:
Рассмотрим каждую из систем отдельно.
При
При указанных значения переменной левая часть неравенства всегда положительна.
при
При указанных значения параметра левая часть неравенства всегда отрицательна.
Таким образом, первая из систем решений не имеет.
Рассмотрим вторую систему:
При
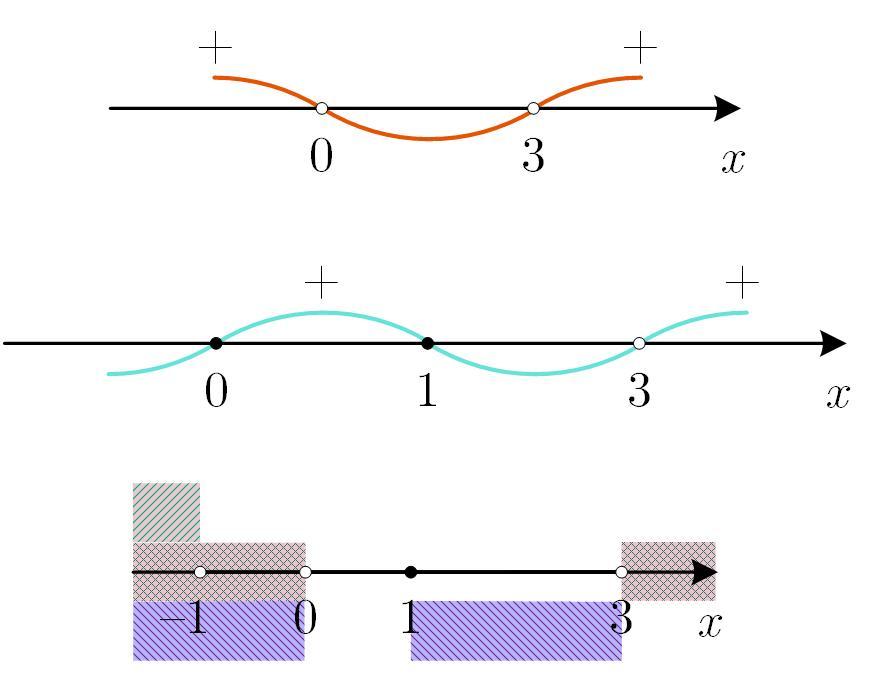
(см. рис.).
При
(см. рис.).
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад