Question

Постройте график функции y=(13x^2-x^4-36)/((x+2)(x-3)) и определите, при каких значениях с прямая у=с имеет с графиком ровно одну общую точку

Answer 1

Область определения функции: $displaystyle left { {{x+2ne0} atop {x-3ne 0}} right. ~~~Rightarrow~~~~ left { {{xne -2} atop {xne 3}} right.$

Упростим заданную функцию

$y=-displaystyle frac{x^4-4x^2-9x^2+36}{(x+2)(x-3)}=- frac{x^2(x^2-4)-9(x^2-4)}{(x+2)(x-3)}=\ \ \ =- frac{(x^2-9)(x^2-4)}{(x+2)(x-3)} =- frac{(x-3)(x+3)(x-2)(x+2)}{(x+2)(x-3)}=-(x+3)(x-2)$

или, раскрывая скобки:  $y=-x^2-x+6$ - парабола, ветви направлены вниз.

m = -b/2a = 1/(-2) = -0.5

y = -0.25 + 0.5 + 6 = 6.25

(-0.5; 6.25) - вершина параболы.

y = c - прямая, параллельная оси Ох.

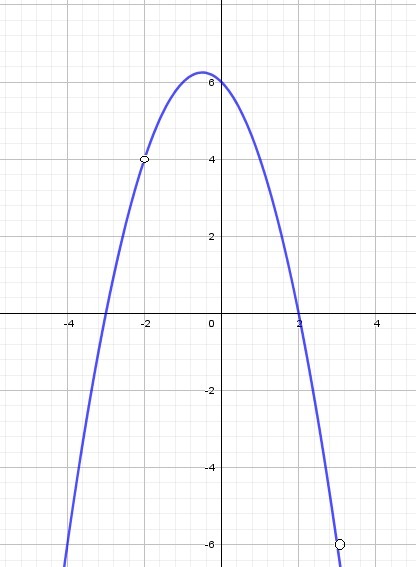
При с = 6,25 графики будут иметь одну общую точку
При c = 4 графики будут иметь одну общую точку
При c = -6 графики будут иметь одну общую точку