Ответы
Ответ дал:
1
Ответ:
Объяснение:
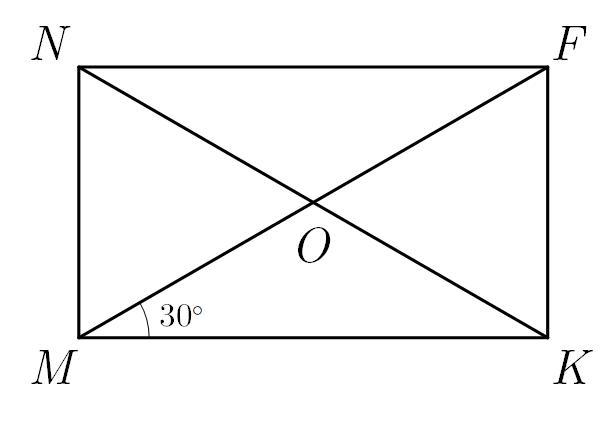
Прямой угол диагональю разбивается на два угла: данный
и
значит
Так как диагонали в прямоугольнике равны и точкой пересечения делятся пополам, то
и треугольник равнобедренный с углом
при основании — следовательно треугольник
равносторонний со стороной 9 см.
Тогда его периметр равен
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад