Question

даю сто баллов пжжжжжжжж помогите срочно нужно☹️☹️☹️

Answer 1

Ответ:

D

Пошаговое объяснение:

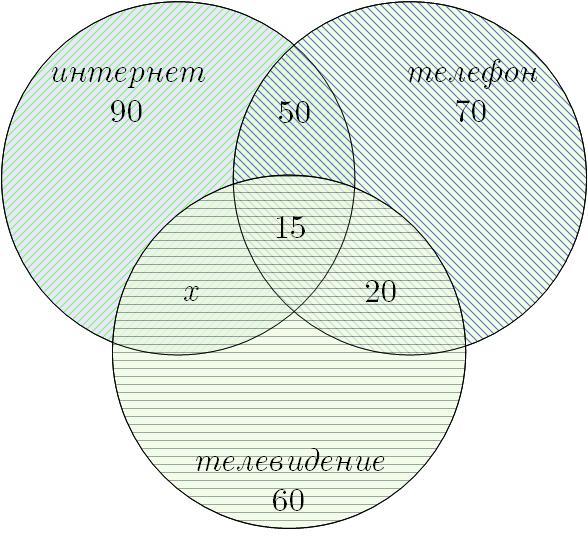
Изобразим условие задачи в виде диаграммы. Пусть кабельное телевидение и интернет имеют $x$ человек (см. рис. 1).

По рисунку видно, что пересечение всех трех услуг (15) входит в каждое из множеств (владельцев каждой услуги по отдельности и владельцев нескольких услуг вместе), отнимем его (см. рис. 2). Теперь видно, что остались пересечения двух услуг по отдельности, они считаются дважды: в количестве владельцев и одной услуги, и второй.

Отнимем эти значения (см. рис. 3). Теперь в каждом из фрагментов кружков написано число, которое входит только в него. Значит можно найти общую сумму людей, которые владеют услугами:

$55 - x + 15 + 55 - x + 35 + x - 15 + 5 + 15 = 165 - x.$

Но по условию задачи владельцев всех услуг $140 - 5 = 135$,

значит

$165 - x = 135;\\\\x = 30.$

Answer 2

Ответ:   30 .

Три множества жителей, имеющих интернет, стац. телефон и кабельное телевидение пересекаются между собой . Изобразим это на чертеже .

Обозначим облаcти полученные при пересечении множеств

через  1 , 2 , 3 , 4 , 5 , 6 , 7 .

Искомое множество жильцов, которые имеют как каб.телевидение, так и интернет обозначим через  х . Это множество состоит из областей  "4" и  "7" . Запишем коротко так:  х="4"+"7" .

По условию:  "5"+"7"=50 чел. ,  "7"=15 чел.    ⇒   "5"=60-15=35 чел.

"7"+"6"=20 чел.  ,  "7"=15 чел.   ⇒   "6" = 20-15=5 чел.

"2"+"5"+"7"+"6"=70   ⇒   "2" = 70-"5"-"7"-"6"=70-35-15-5=15 чел.

"3"+"4"+"7"+"6"=60   ⇒   "3" = 60-"4"-"7"-"6"=60-(х-15)-15-5=55-х  чел.

"1"+"5"+"7"+"4"=90   ⇒    "1" = 90-"5"-"7"-"4"=90-35-15-(х-15)=55-х чел.

Так как по условию всего жителей 140чел.  и 5 человек не имеют ни интернета, ни стац.телефона, ни каб.телевидения , то сумма жителей, имеющих эти услуги равна 140-5=135 чел.

Запишем сумму в виде уравнения.

(55-х)+35+15+(х-15) + 15+5 + (55-х)=135

165-х=135

х=165-135

х=30