Ответы
Ответ дал:
0
Ответ:
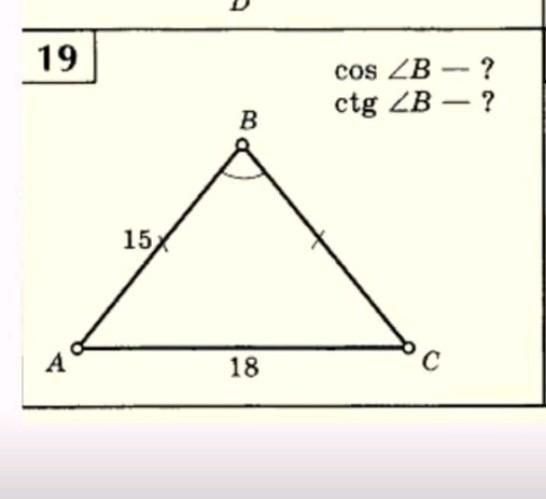
cos∠B=7/25
ctg∠B = 7/24
Объяснение:
Воспользуемся теоремой косинусов:
Через основное тригонометрическое тождество найдем синус В
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад