Question

Найдите площадь равнобедренного треугольника. Угол при вершине, противолежащей основанию равен 45, боковая сторона треугольника равна корень из 14 .

Answer 1

Ответ:

3,5√2 кв. ед.

Объяснение:

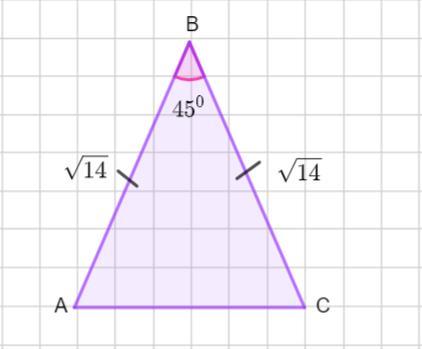
Найти площадь равнобедренного треугольника. Угол при вершине, противолежащей основанию равен 45 °, боковая сторона равна √14.

Пусть дан ΔАВС - равнобедренный. АВ =ВС = √14 ед., ∠В =45°.

Площадь треугольника равна полупроизведению двух его сторон на синус угла между ними.

Тогда

$S =\dfrac{1}{2} \cdot AB \cdot BC \cdot sin B;\\\\S =\dfrac{1}{2} \cdot \sqrt{14} \cdot \sqrt{14} \cdot sin 45^{0}= \dfrac{1}{2} \cdot 14 \cdot \dfrac{\sqrt{2} }{2} = \dfrac{7\sqrt{2} }{2}=3,5 \sqrt{2}$

Значит, площадь треугольника равна 3,5√2 кв. ед.

Answer 2

Ответ:

7√2/2 ед²

Объяснение:

Площадь треугольника равна половине произведения сторон на синус угла между ними.

S=1/2 * √14 * √14 * sin45 = 1/2 * 14 * √2/2 = 7√2/2 ед²