Question

ПОМОГИТЕ ДАМ 40 БАЛЛОВ

Answer 1

Ответ:

Доказано: АВ || DE.

Объяснение:

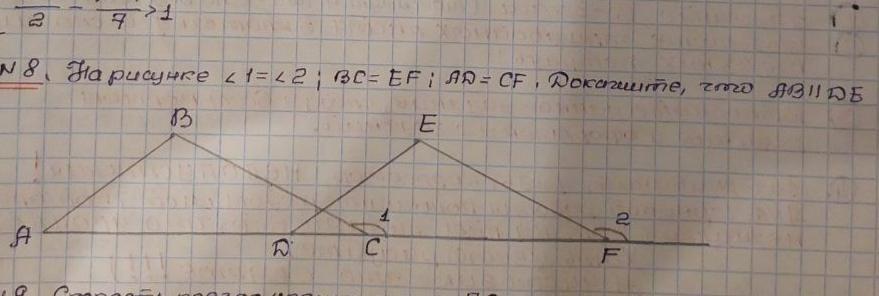
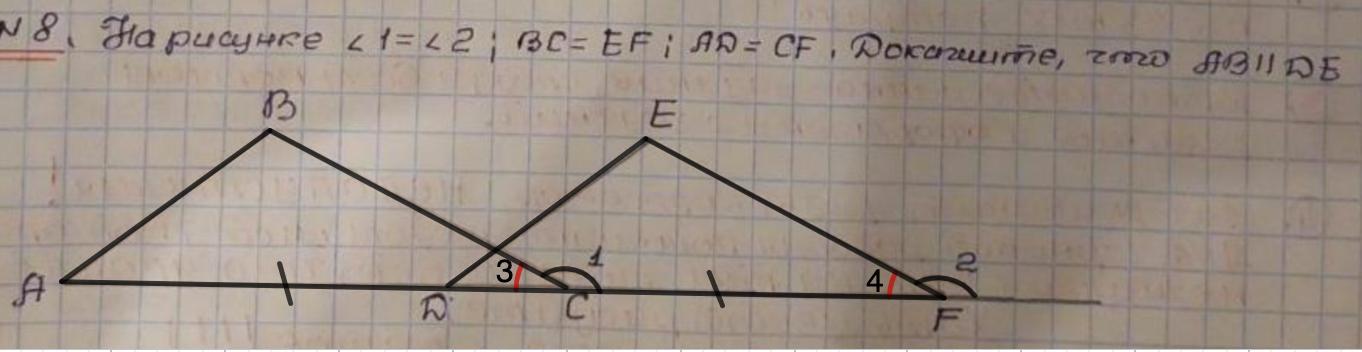
На рисунке ∠1 = ∠2; BC = EF; AD = CF. Докажите, что AB || DE.

Дано: ΔАВС, ΔDEF.

∠1 = ∠2; BC = EF; AD = CF;

Доказать: AB || DE.
Доказательство:

Рассмотрим ΔАВС и ΔDEF.

BC = EF (условие)

АС = AD + DC

DF = CF + DC

AD = CF (условие)

⇒ АС = DF

• Сумма смежных углов равна 180°.

⇒ ∠3 = 180° - ∠1  (смежные)

∠4 = 180° - ∠2 (смежные)

∠1 = ∠2 (условие)

⇒ ∠3 = ∠4

⇒ ΔАВС = ΔDEF (по двум сторонам и углу между ними, 1 признак)

• В равных треугольниках против равных сторон лежат равные углы.

⇒ ∠ВАС = ∠EDF - соответственные при АВ и DE  и секущей АF.

• Если при пересечении двух прямых третьей соответственные углы равны, то эти прямые параллельны.

⇒ АВ || DE.