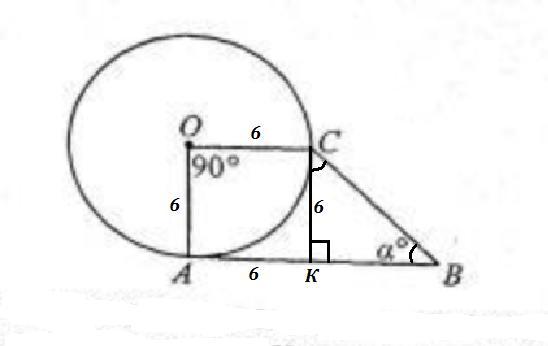
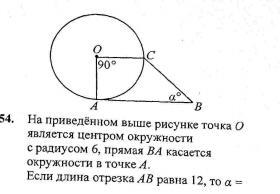
На приведенном ниже рисунке точка О является центром окружности с радиусом 6 прямая BA касается окружности в точке А. Если длина отрезка AB равна 12, то чему равен угол a?
Ответы
Пошаговое объяснение:
касательная к окружности перпендикулярна радиусу,проведенному в точку касания, значит ∠А=90°.
АОСВ - прямоугольная трапеция.
АО=ОС=6 -как радиусы
АВ=12
Чертим СН - высоту
∆ СНВ - прямоугольный:
СН=АО=6
НВ=АВ-АН=АВ-ОС=12-6=6
tgα=CH/HB=6/6=1
α=45°
ответ: 45°
Решение.
Центр окружности - точка О , радиус окружности R=6 .
ВА - касательная к окружности в точке А ⇒ ∠ОАВ=90° и ОА⊥ АВ .
АВ=12 , ∠АОС=90° .
Проведём перпендикуляр СК к АВ , СК⊥АВ , ∠СКА =90° .
Тогда ОА || СК и три угла в четырёхугольнике АКСО равны по 90° , значит АКСО - квадрат .
ОА=СК=6 , ОС=АК=6 ⇒ ВК=АВ-АК=12-6=6
В ΔСКВ угол ∠СКВ=90° и СК=ВК=6 , значит ΔСКВ - прямоугольный равнобедренный треугольник ⇒ ∠СВК=∠ВСК=α .
Сумма острых углов в прямоугольном треугольнике равна 90° ,
∠СВК+∠ВСК=90° ,
значит α=∠СВК=∠ВСК=90°:2=45°
Ответ: α=45° .