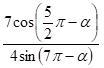Ответы
Ответ дал:
1
Ответ:
1,75 - значение выражения.
Пошаговое объяснение:
Найти значение выражения
Воспользуемся периодичностью синуса и косинуса :
Воспользуемся формулами приведения
и получим
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад