Question

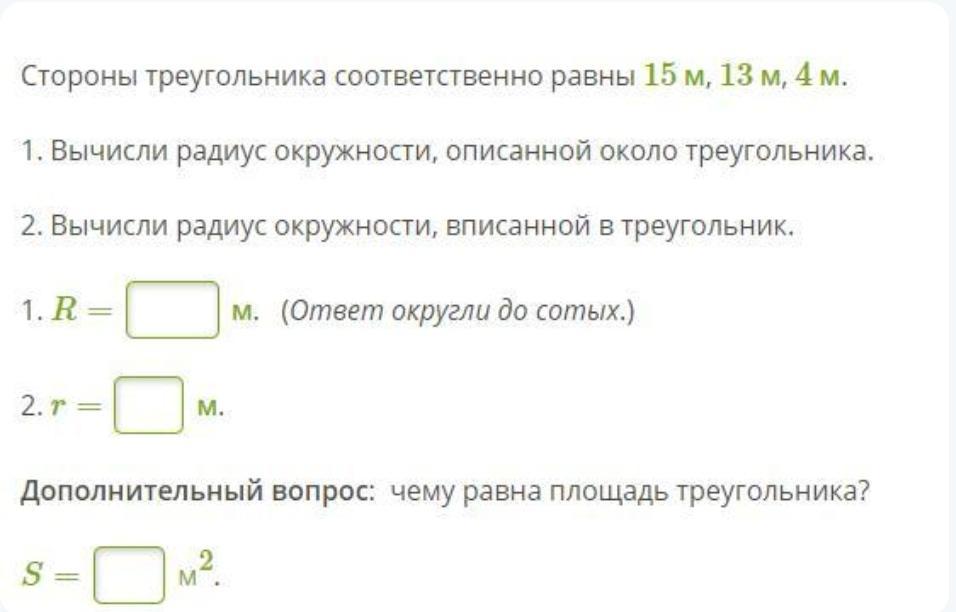
Стороны треугольника соответственно равны 15 м, 13 м, 4 м.
1. Вычисли радиус окружности, описанной около треугольника.

2. Вычисли радиус окружности, вписанной в треугольник.

Answer 1

Объяснение:

S∆=√(p(p-a)(p-b)(p-c));

p=(a+b+c)/2=(15+13+4)/2=32/2=16 м полупериметр.

S∆=√(16(16-15)(16-13)(16-4))=

√(16*1*3*12)=4*6=24 м²

r=S∆/p=24/16=1,5 м

R=(abc)/4S∆=(15*13*4)/4*24=780/96=8,125 м

Ответ:

R=8,125м

r=1,5 м

S=24 м²

Answer 2

***

поскольку нам известны 3 стороны треугольника =>

найдем площадь треугольника по теореме Герона:

$\displaystyle \bf S=\sqrt {p(p-a)(p-b)(p-c)}$,

где a, b и c - стороны,

p - полупериметр,

$\displasytyle \bf P=a +b+c$

=>

$\displaystyle \bf p=\frac{a+b+c}{2}=\frac{15+13+4}{2}=\frac{32}{2}=16$

$\displaystyle \bf S=\sqrt {p(p-a)(p-b)(p-c)}\\\\\\S=\sqrt {16\cdot (16-15)(16-13)(16-4)}=\sqrt{16\cdot 1\cdot 3\cdot 12} =\sqrt{576} =24 \ (m^2)$

$\boxed{\displaystyle \bf \Big \ S=24 \ (m^2)}$

из формулы  для нахождения площади треугольника через радиус вписанной окружности:

$\displaystyle \bf S= rp$

• (площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.)

находим радиус:

$\displaystyle \bf r=\frac{S}{p}=\frac{24}{16} =1,5 \ (m)$

$\boxed{ \Big \ \displasytyle \bf r=1,5 \ (m)}$

$\displaystyle \bf R=\frac{abc}{4S}=\frac{15\cdot 13 \cdot 4}{4 \cdot 24}}=\frac{780}{96} =8,125 \ (m)$

$\boxed{ \Big \ \displaystyle \bf R=8,125 \ (m)}$