Не понимаю как решить
в прямоугольном треугольнике abc с прямым углом B проведены высота bh медиана bm и биссектриса BL. Оказалось что abh=22∘
HBL =
MBC =
Ответы
Ответ дал:
0
Ответ:
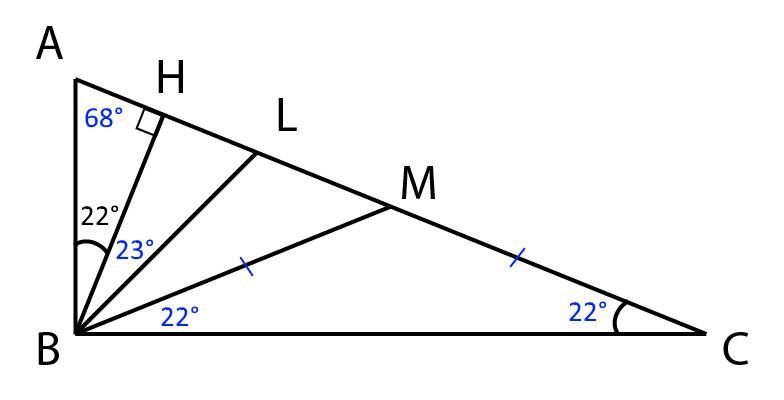
∠HBL = 23°, ∠MBC = 22°
Объяснение:
Дано:
∠B = 90°
BH - высота
BM - медиана
BL - биссектриса
∠ABH = 22°
∠HBL - ?
∠MBC - ?
-------
1) BL - биссектриса, поэтому ∠ABL = ∠ABC/2 = 45°
∠HBL = ∠ABL-∠ABH = 45-22 = 23°
2) Из прямоугольного треугольника ABH ∠HAB = 90-∠ABH = 68°.
Из прямоугольного треугольника ABC ∠ACB = 90-∠HAB = 22°.
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы, поэтому:
BM = AC/2 = AM = MC
Треугольник BMC - равнобедренный, поэтому
∠MBC = ∠MCB = 22°
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад