Question

найдите площадь ромба если сторона его равна 4, а угол равен 60°. Нужен ответ без формулы синуса

Answer 1

Ответ:

S(ABCD)=8√3 ед²

Объяснение:

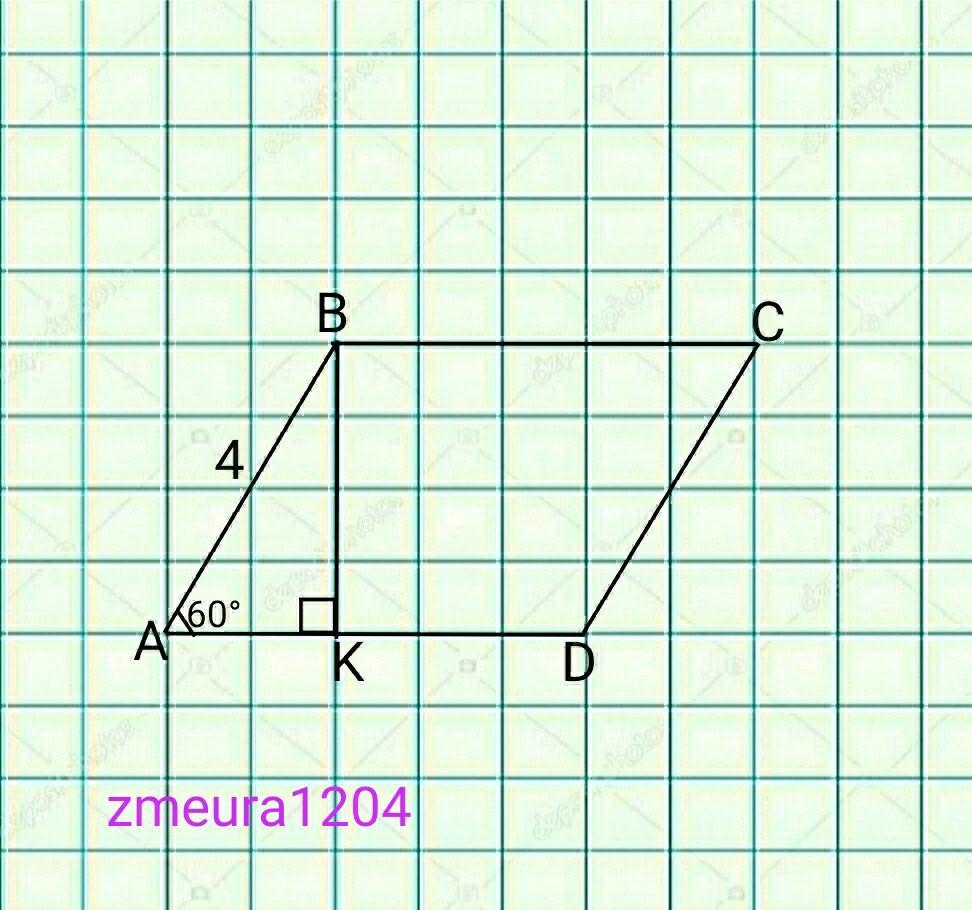
Решение 1)

∆АВК- прямоугольный треугольник.

∠ВАК=60°; ∠ВКА=90°; ∠АВК=30°

АК- катет против угла ∠АВК=30°

АК=АВ/2=4/2=2 ед

Теорема Пифагора:

ВК=√(АВ²-АК²)=√(4²-2²)=√((4-2)(4+2))=

=√(2*6)=2√3 ед.

S(ABCD)=BK*AD=4*2√3=8√3 ед².

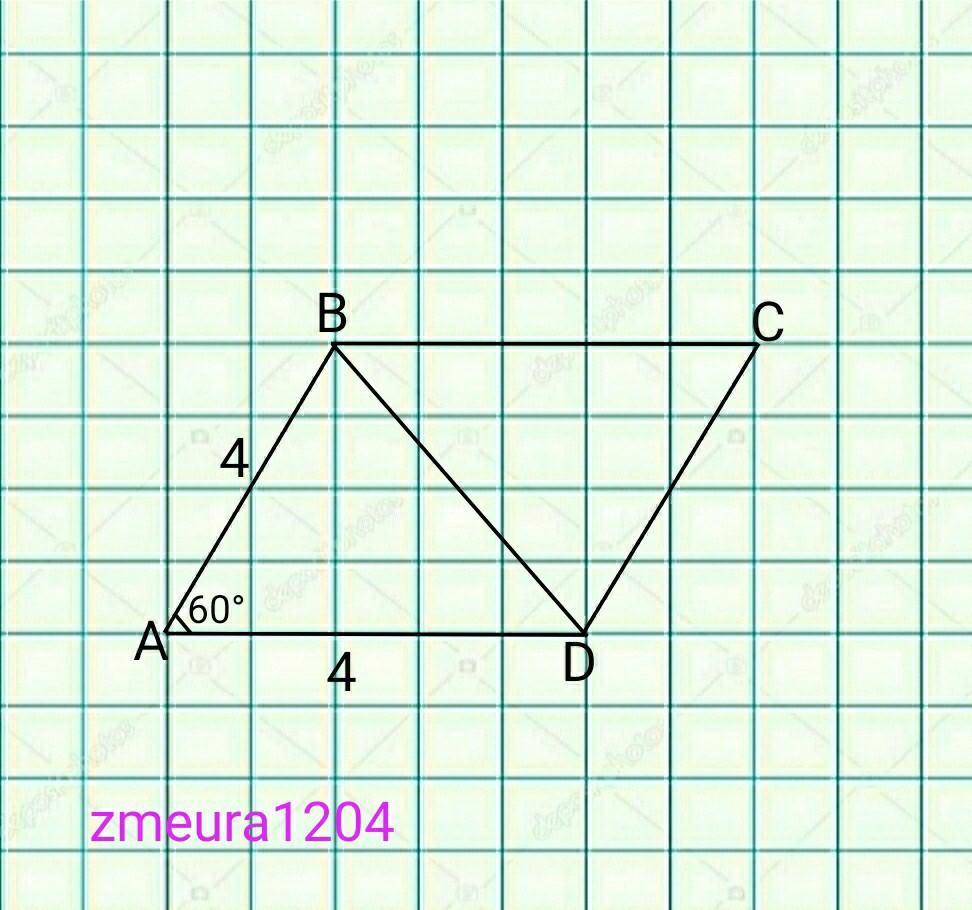
Решение 2)

В ромбе с углами 60°; 120° меньшая диагональ равна стороне ромба.

ВD=AB;

∆ABD- равносторонний треугольник

S(∆ABD)=AB²√3/4=4²√3/4=4√3 ед²

S(ABCD)=2*S(∆ABD)=2*4√3=8√3 ед.