Ответы
Ответ дал:
2
Ответ:
∠ВОС=10°
Объяснение:
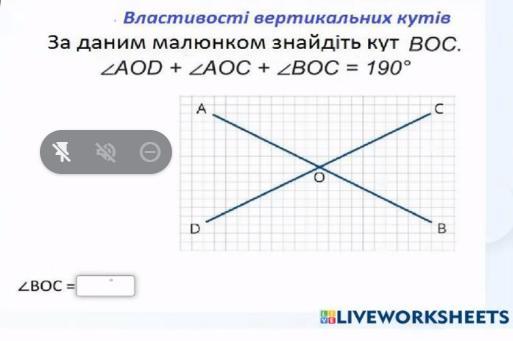
За малюнком треба знайти кут ВОС, якщо ∠AOD+∠AOC+∠BOC=190°
- При перетині двох прямих утворюються дві пари вертикальних кутів і чотири пари суміжних кутів.
- Вертикальними називаються два кути, сторони одного з яких є додатковими променями до сторін другого кута.
- Вертикальні кути рівні.
- Суміжними називаються два кути,одна сторона яких спільна, а дві інші утворюють пряму, тобто є доповняльними променями.
- Сума суміжних кутів дорівнює 180°.
Прямі АВ і CD перетинаються в точці О.
Утворились дві пари вертикальних кутів: ∠AOD=∠BOC, ∠AOC=∠BOD, та чотири пари суміжних кутів: ∠AOD+∠AOC=180°, ∠AOC+∠BOC=180°, ∠BOC+∠BOD=180°, ∠BOD+∠AOD=180°.
За умовою: ∠AOD+∠AOC+∠BOC=190°, тому:
#SPJ1
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад