Question

в равнобедренной трапеции ABCD косинус острого угла равен дроби 1/2,а основания относятся как 3:1.Найдите площадь трапеции,если бококвая сторона равна 12 см

Answer 1

Ответ:

72√3 см²

Объяснение:

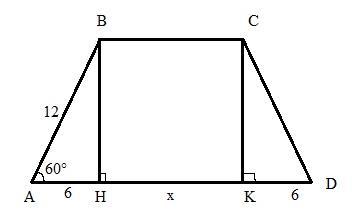
Пусть BH и CК - высоты, НК=х.

cosBAН=1/2 => <BAН=60°, <АВН90-60=30°, АН=1/2*АВ=1/2*12=6см.

AH=KD=6см. ВС=НК=х.

AD:BC=3:1 => (x+2*6)/x=3

3x=x+12

2x=12

x=6

BC=6см, AD=6+12=18см.

ВН=AB*sin60=12*√3/2=6√3см

S(ABCD)=(AD+BC)*BH/2=(6+18)*6√3/2=72√3 см²