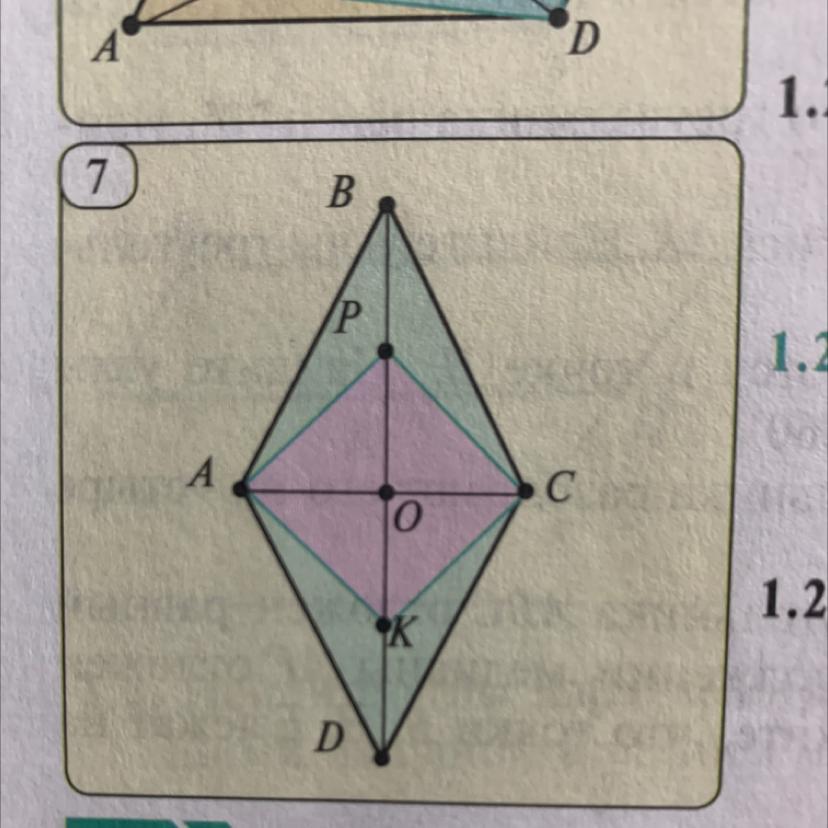
На диагонали BD параллелограмма ABCD
выбраны точки Р и К (рис.7). Докажите, что четырехугольник АРСК - параллелограмм,
если BP=KD
Приложения:
Ответы
Ответ дал:
1
Ответ:
Объяснение:
ABCD - параллелограмм => AO=OC и BO=OD.
Поскольку BP=KD, то и BO-BP=OD-KD, то есть PO=ОК.
Но РК и АС - также диагонали четырехугольника АРСК, и они в точке пересечения делятся пополам. А значит четырехугольник АРСК - параллелограмм.
Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
dlyagoogla229:
спасибо
Вас заинтересует
2 года назад
7 лет назад