Question

Помогите пожалуйста оооочень надо

Answer 1

Ответ:

  $\bf f(x)=\sqrt{40+6x-x^2}$  

$40+6x-x^2=-(x^2-6x-40)=-((x-3)^2-9-40)=\bf 49-(x-3)^2$  ⇒

1)  ООФ:

 $49-(x-3)^2\geq 0\ \ ,\ \ (x-3)^2-49\leq 0\ \ ,\ \ (x-3-7)(x-3+7)\leq 0\ ,$

$(x-10)(x+4)\leq 0\ \ \Rightarrow \ \ \ \bf x\in [-4\ ;\ 10\ ]$  

2)  МЗФ:

Так как функция - это кв. корень , то известно, что кв. корень из какого-либо выражения - величина неотрицательная,  $y\geq 0$  .

Квадратный трёхчлен  $40+6x-x^2=49-(x-3)^2$  принимает своё наибольшее значение в вершине параболы при х=3, это значение равно у=49 . При извлечении кв. корня, наибольшим значением будет у=7 . Поэтому множество значений функции

$\bf y\in [\ 0\ ;\ 7\ ]$

3)  Нули функции:   $\sqrt{40+6x-x^2}=0\ \ ,\ \ \ \sqrt{49-(x-3)^2}=0\ \ \Rightarrow$

$49-(x-3)^2=0\ \ ,\ \ (7-x+3)(7+x-3)=0\ \ ,\ \ (10-x)(x+4)=0\ ,\\\\\bf x_1=-4\ ,\ x_2=10$

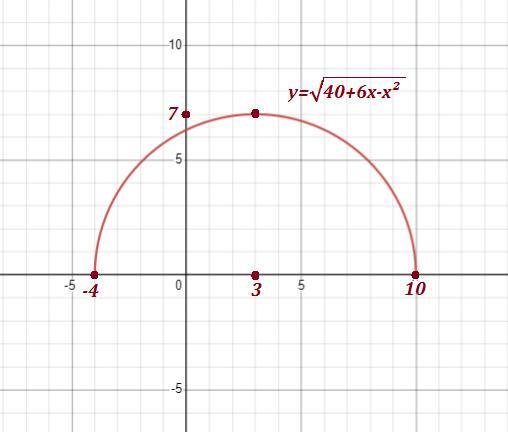
7)  Сначала построим график.

$y=\sqrt{49-(x-3)^2}\ \ \to \ \ y^2=49-(x-3)^2\ \ ,\ \ \bf (x-3)^2+y^2=7^2\ ,\ y\geq 0$

Это окружность с центром в точке (3;0) и радиусом R=7 . Так как у≥0 ,

то от этой окружности берём только ту часть, которая лежит  выше оси ОХ . Значит, графиком является полуокружность с центром в точке (3;0) и  радиусом R=7 .

4)  Функция возрастает при  $\bf x\in [-4\ ;\ 3\ ]$  .

5)  Промежутки знакопостоянства функции.

Функция всюду на обл. определения неотрицательна, то есть при  

$x\in [-4\ ;\ 10\ ]$  значения функции   $y\geq 0$  .

6)  Минимум $y=0$  функция достигает при  $x=-4$  и  $x=10$  .

Максимум  $y=7$  функция достигает при  $x=3$  .