Question

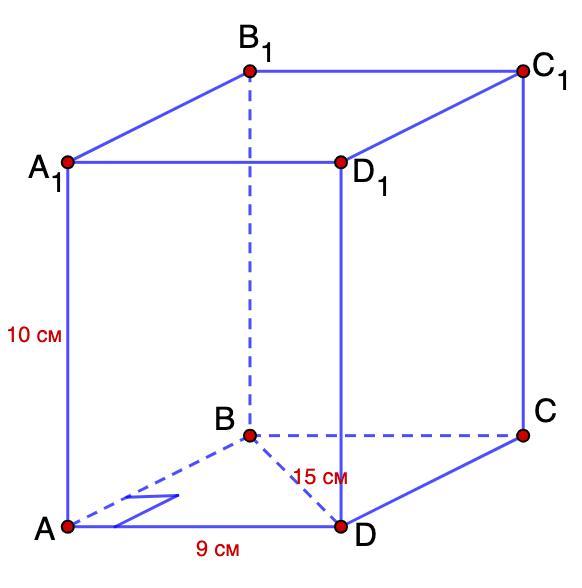
1. В основі прямої призми лежить прямокутник, сторона якого дорівнює 9 см, а діагональ 15 см. Бічне ребро призми дорівнює 10 см. Обчислити площу бічної поверхні призми ​

Answer 1

Ответ:

Площадь боковой поверхности призмы равна 420 см².

Объяснение:

1. В основе прямой призмы лежит прямоугольник, сторона которого равна 9 см, а диагональ 15 см. Боковое ребро призмы равно 10 см. Вычислить площадь боковой поверхности призмы.

Дано: ABCDA₁B₁C₁D₁ - прямая призма;

ABCD - прямоугольник;

AD =9 см; BD = 15 см; АА₁ = 10 см.

Найти: Sбок.

Решение:

• Площадь боковой поверхности призмы равна произведению периметра основания на высоту.

Рассмотрим ΔABD - прямоугольный.

AD =9 см; BD = 15 см.

По теореме Пифагора найдем АВ:

АВ² = BD² - AD² = 225 - 81 = 144

АВ = √144 = 12 (см)

• Периметр прямоугольника равен полусумме смежных сторон.

Р(ABCD) = 2 (AB + AD) = 2(12 + 9) = 42 (см)

Теперь можем найти Sбок.:

Sбок. = Р(ABCD) · АА₁ = 42 · 10 = 420 (см²)

Площадь боковой поверхности призмы равна 420 см².

#SPJ1