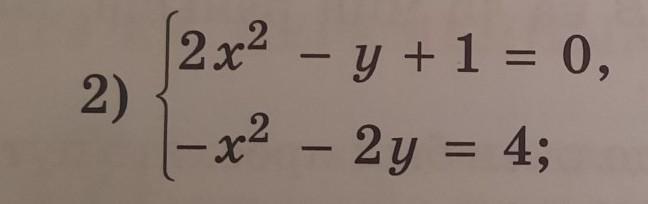Ответы
Ответ дал:
3
квадрат числа на множестве действительных чисел всегда неотрицателен, а значит некомплексных решений система не имеет
Ответ дал:
0
Поскольку левая часть всегда отрицательная, а правая всегда положительная утверждение ложно для любого х
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад