Question

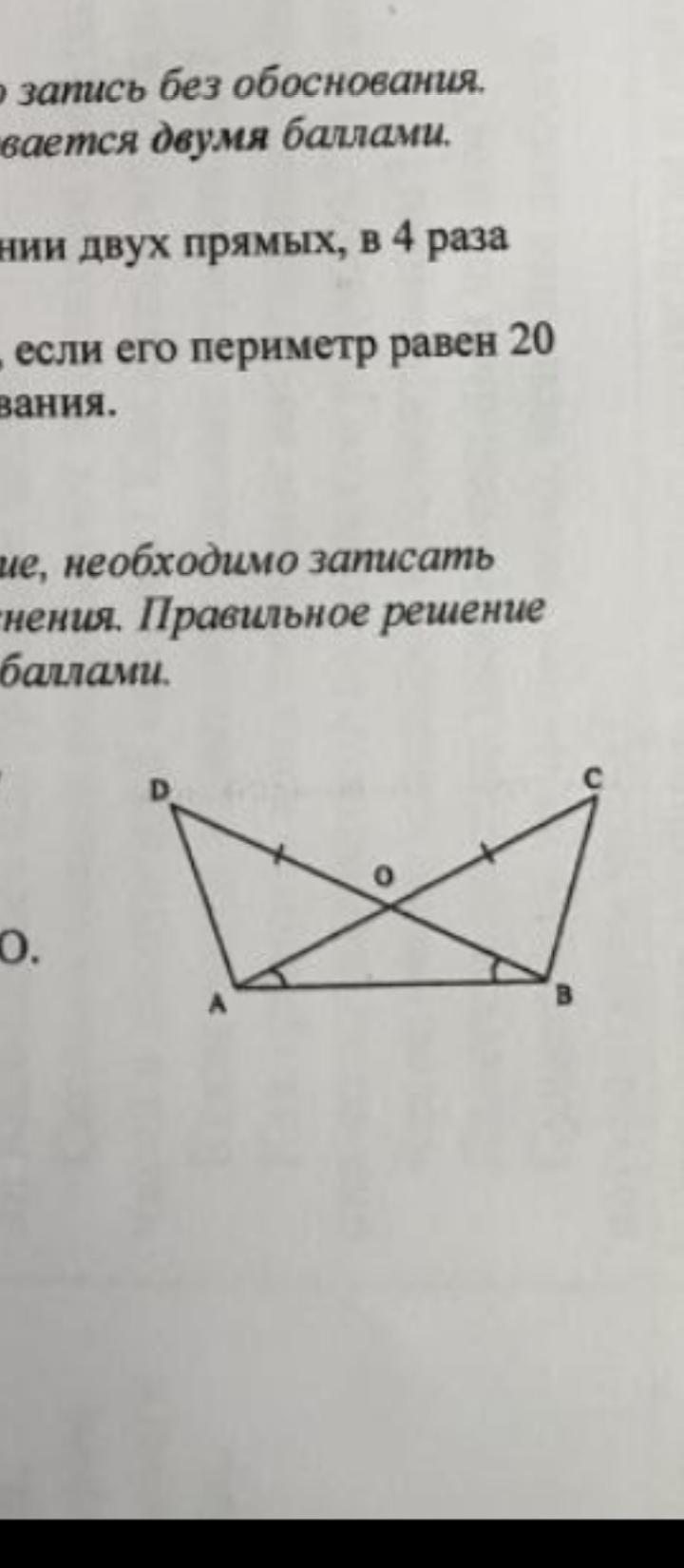
Треугольнике ACB и BDA имеют общую основу AB, отрезки AC и BD пересекают в точке О ,известно что AC равно BD, угол ABD = угол

BAC,докажите что треугольник DAO = треугольнику CBO.
ОБЯЗАТЕЛЬНО ОТМЕТИТЬ ВСЁ НУЖНОЕ НА РИСУНКЕ!!

Answer 1

Ответ:

Доказали, что ΔDAO = ΔCBO.

Объяснение:

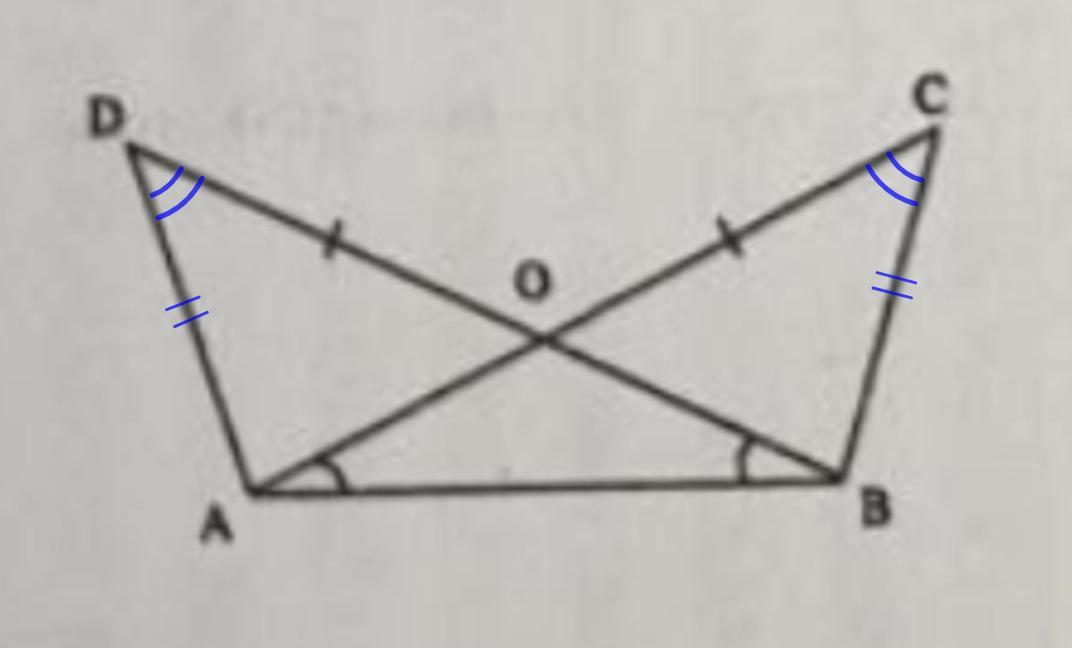
Треугольники ACB и BDA имеют общую основу AB, отрезки AC и BD пересекают в точке О ,известно что AC равно BD, угол ABD = углу BAC. Докажите, что треугольник DAO = треугольнику CBO.

Дано: ΔACB и ΔBDA.

AC ∩ BD = О; AC = BD;

∠ABD = ∠BAC.

Доказать: ΔDAO = ΔCBO.

Доказательство:

1. Рассмотрим ΔACB и ΔBDA.

По условию: АВ - общая; AC = BD; ∠BAC = ∠ABD.

⇒ ΔACB и ΔBDA (по двум сторонам и углу между ними, 1 признак)

• В равных треугольниках равны соответственные элементы.

⇒ AD = BC; ∠D = ∠C.

2. Рассмотрим ΔАОВ.

∠BAC = ∠ABD (условие)

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ АО = ОВ

3. Рассмотрим ΔDAO и ΔCBO.

AD = BC; ∠D = ∠C (п.1)

OD = DB - OB

OC = AC - AO

AC = BD (условие); АО = ОВ (п.2)

⇒ OD = ОС.

ΔDAO = ΔCBO (по двум сторонам и углу между ними, 1 признак)

Что и требовалось доказать.