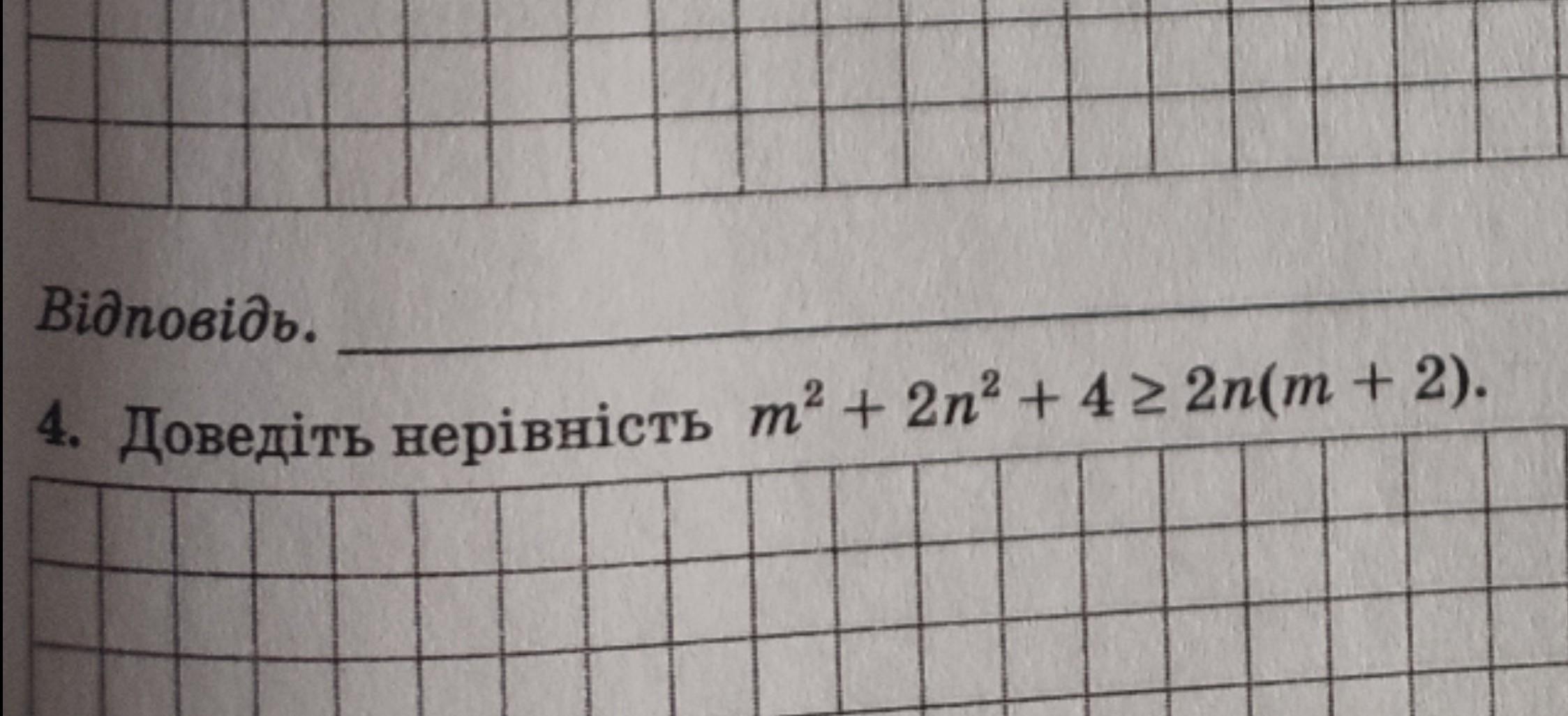Ответы
Ответ дал:
1
Відповідь:
Пояснення:
4 . m² + 2n² + 4 ≥ 2n( m + 2 ) .
Cкладемо різницю лівої і правої частин нерівності і спростимо :
m² + 2n² + 4 - 2n( m + 2 ) = m² + 2n² + 4 - 2nm - 4n = ( m² - 2mn + n² ) +
+ ( n² - 4n + 4 ) = ( m - n )² + ( n - 2 )² ≥ 0 як сума двох квадратів .
Отже , дана нерівність правильна при будь - яких значеннях m i n .
kovalchuktymur221:
от души братик
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад
9 лет назад