Question

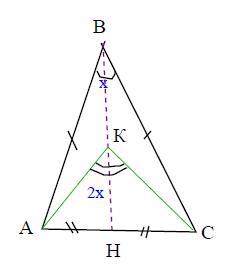
В равнобедренном треугольнике ABC, где AB=BC, провели высоту BH и выбрали на ней такую точку K, что ∠AKC=2∠ABC. Докажите, что 2AK меньше, чем ВН + АС/2

Answer 1

Ответ:

Объяснение:

Дано:

ΔАВС, АВ=ВС

ВН -высота, ВН⊥АС

∠AKC=2∠ABC

Док., 2АК < (ВН +АС/2)

-------------------
1) Пусть ∠ABC = х°, тогда ∠AKC = 2х°

2), Т.к. высота в прямоугольном Δ-ке является медианой и биссектрисой, то
АН = НС и ∠АВН =∠НВС = х°/2

Точка К лежит на серединном перпендикуляре (АН = НС и ВН⊥АС), следовательно,

ΔАКС тоже равнобедренный и ∠АКН = ∠НКС = 2х/2 = х°

3) Рассм. прямоугольные ΔКНА и ΔВНА ( ВН⊥АС по условию)

Т.к. сумма углов Δ-ка = 180°, то из ΔКНА:

∠КАН = 180° - 90° - х = 90° - х°

из ΔВНА:   ∠ВАН = 90° - х/2

Тогда ∠ВАК = ∠ВАН - ∠КАН = 90° - х°/2 -(90° - х°) = х°/2

4) Т.о. , получили, что в ΔАКВ ∠ВАК = ∠АВК = х°/2, т.е

ΔАКВ - равнобедренный и АК =ВК

5) Сумма 2-х  сторон в Δ-ке всегда больше 3-ей, т.е.

АК +ВК > АВ или 2АК > АВ

В свою очередь из ΔАВН следует, что АВ < ВН+АН или

АВ < ВН + АС/2

6) ВН + АС/2 < АВ < 2АК

2АК > ВН + АС/2

Получилось, что больше.