Question

СРОЧНО! Медiана рiвнобедреного трикутника, проведена до основи, дорiвнос 25 см. Обчисліть площу трикутни ка, якщо площа вписаного в нього кола 64π см².

Answer 1

Ответ:

$333\dfrac{1}{3}$  см²

Объяснение:

Площадь круга:

S = πr²

64π = πr²

r² = 64

r = 8 см

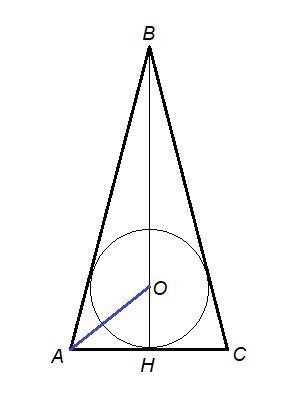
• В равнобедренном треугольнике медиана, проведенная к основанию, является высотой и биссектрисой.

Центр вписанной в треугольник окружности - точка О - точка пересечения биссектрис. Значит она лежит на медиане ВН.

О так как ВН⊥АС, то ОН = r = 8 см - радиус вписанной окружности.

ВО = ВН - ОН = 25 - 8 = 17 см

Свойство биссектрисы треугольника:

• биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

АО - биссектриса ΔАВС, а значит и ΔАВН. Тогда

$\dfrac{AB}{AH}=\dfrac{BO}{OH}=\dfrac{17}{8}$

Если х - коэффициент пропорциональности (x > 0), то

АВ = 17х,  АН = 8х.

Из прямоугольного треугольника АВН по теореме Пифагора:

AB² - AH² = BH²

(17x)² - (8x)² = 25²

289x² - 64x² = 625

225x² = 625

$x^2=\dfrac{625}{225}$

$x=\dfrac{25}{15}=\dfrac{5}{3}$

$AC=2AH=2\cdot 8\cdot \dfrac{5}{3}=\dfrac{80}{3}$  см

Площадь треугольника АВС:

$S=\dfrac{1}{2}AC\cdot BH$

$S=\dfrac{1}{2}\cdot \dfrac{80}{3}\cdot 25=\dfrac{1000}{3}=333\dfrac{1}{3}$  см²