Ответы
Если при пересечении двух прямых и секущих, внутренние накрест лежащие углы равны => прямые параллельные ;
∠BKL = ∠KLD => BC || AD ;
∠BMN = ∠MND => AB || DC ;
BC || AD, AB || DC => ABCD - параллелограмм (по признаку параллелограмма : если противоположные стороны четырехугольника попарно параллельны => этот четырехугольник параллелограмм).
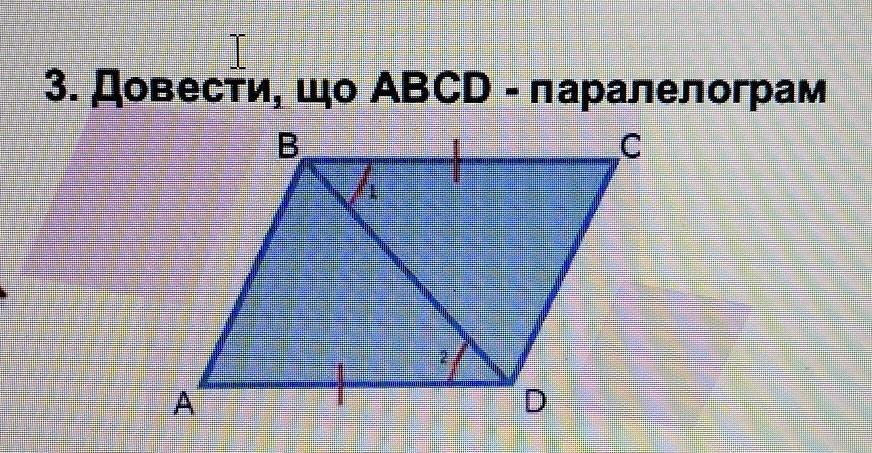
На українській мові :
Якщо при перетині двох прямих і січних, внутрішні навхрест лежачі кути рівні => прямі паралельні ;
∠BKL = ∠KLD => BC || AD ;
∠BMN = ∠MND => AB || DC ;
BC || AD, AB || DC => ABCD - паралелограм (за ознакою паралелограма: якщо протилежні сторони чотирикутника попарно паралельні => цей чотирикутник паралелограм).
думаю помогло
Ответ:
дано
BC=AD
BC || AD
BD - спільна
∆ADB = ∆CBD
доведення
Якщо в чотирикутнику кожні дві протилежні сторони рівні, то цей чотирикутник - паралелограм.
кут 1 і 2 рівні як різносторонні при паралельних прямих BC i AD.
Отже трикутники ADB i CBD рівні за першою ознакою рівності трикутників, звідси AB = CD.
Таким чином у чотирикутнику ABCD кожні дві протилежні сторони рівні. Отже ABCD - паралелограм.
Объяснение:
Я не знаю правильно це чи ні, але якщо не правильно то вибач(