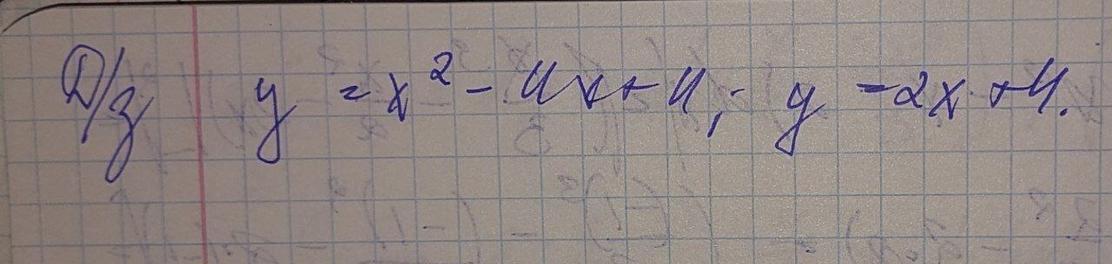Ответы
Ответ дал:
1
Відповідь:
(x1, y1) = (6, 16), (x2, y2) = (0, 4)
Покрокове пояснення:
1. Знайдемо х. Прирівняємо рівняння одне до одного:
Тобто, х = 6 і х = 0.
2. Знайдемо у підставляючи значення х у рівняння.
Якщо x = 6, то:
Якщо х = 0, то:
Маємо такі відповіді: (6, 16) i (0, 4).
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад