Основою піраміди є рівнобедрений трикутник, бічна сторона якого дорівнює 3 корень 10 см, а основа - 6см. Висота піраміди дорівнює 5см, а її бічні ребра є рівними. Знайдіть бічне ребро піраміди
Ответы
Ответ дал:
4
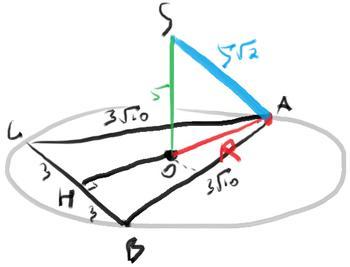
Опустим высоту пирамиды. Видим, что она образует с боковыми ребрами равные прямоугольные треугольники (по катету и гипотенузе). Следовательно, основание высоты равноудалено от вершин треугольника основания. То есть, высота падает в центр (O) описанной окружности основания. Найдем её радиус (OA).
Рассмотрим основание ABC. Высота AH является медианой (треугольник р/б) и по теореме Пифагора равна 9 (из прямоугольного треугольника AHB со сторонами 3 и 3v10).
sinB =AH/AB =9/3v10 =3/v10
По теореме синусов
2R= AC/sinB =3v10 : 3/v10 => R=5 =OA
Из треугольника SAO (SO=OA=5) по теореме Пифагора SA=5v2
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад