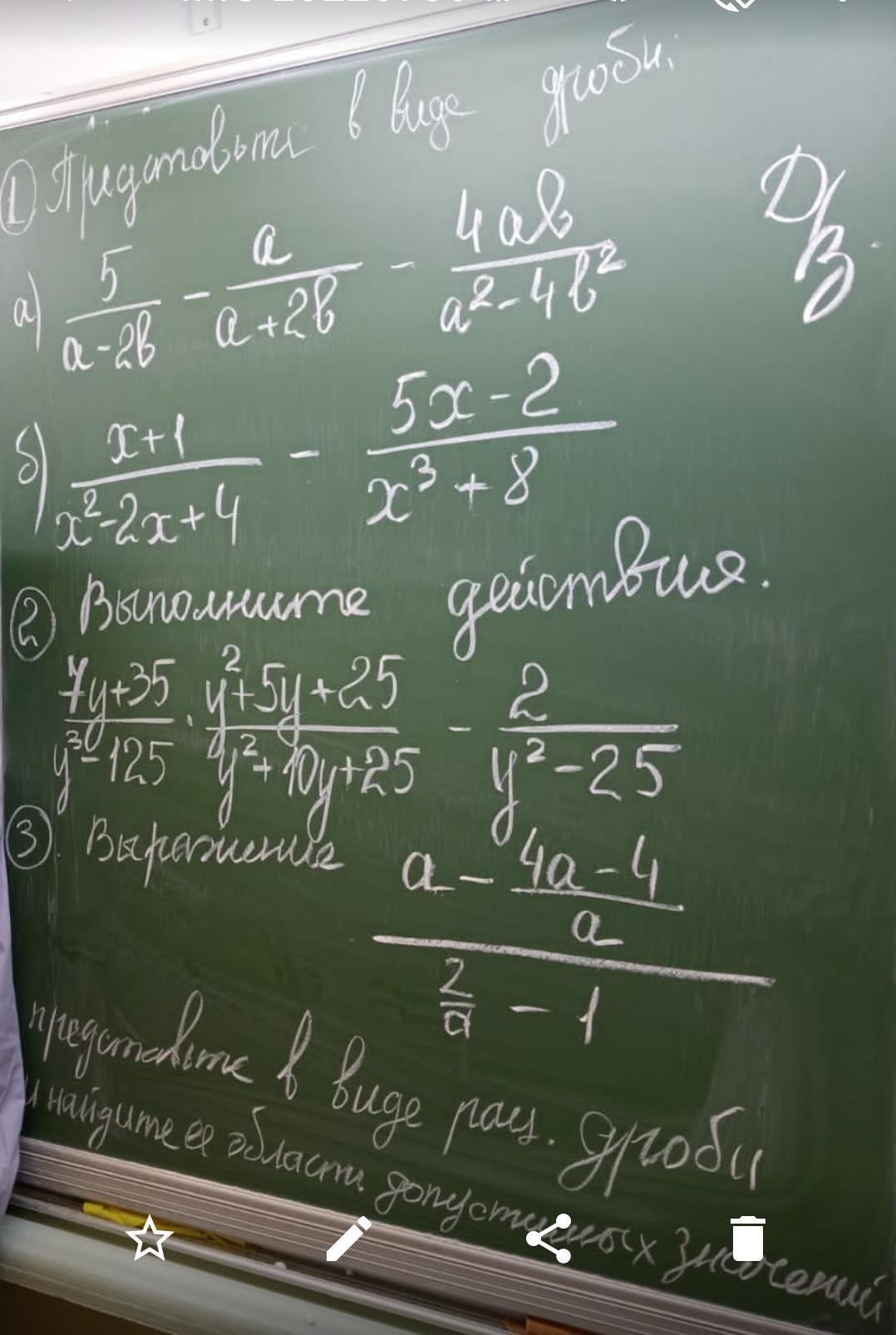Ответы
Ответ дал:
2
Ответ:
Чтобы сумму или разность дробей представить в виде одной дроби, надо привести дроби к общему знаменателю, разложив знаменатели заданных дробей на множители .
ОДЗ:
duravkinoleg:
Во втором задании у на же нету x. И как x2+5y+25 сокращённо с y2+5y+125?
Я посмотрел внимательней и вижу 25 вначале, а потом 125. Ну а так спасибо за работу
описка
исправлю , у и 25 должно быть
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад