Question

ДОПОМОЖІТЬ БУДЬ ЛАСКА

Answer 1

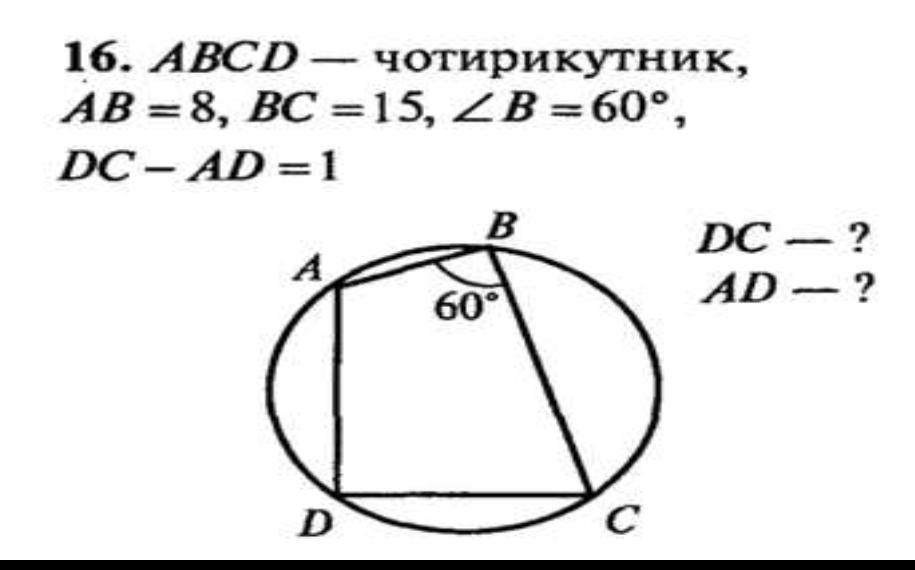
Находим АС по теореме косинусов:

АС = √(8² + 15²- 2*8*15*cos60°) = √(64 + 225 – 240*(1/2)) =

     = √169 = 13.

Сумма углов B и D равна 180 градусов, поэтому D = 180 – 60 = 120 градусов.

Примем AD за х, тогда CD = х + 1.

Применим ту же теорему косинусов.

АС = √(x² + (x + 1)² - 2*x*(x + 1)*cos120°)

√( x² + x² + 2x + 1 – (2x² + 2x)*(-1/2)) =

     = √(2x² + 2x + 1 + x² + x) =

     = √(3x² + 3x + 1).

Приравняем это выражение АС и возведём обе части в квадрат.

169 = 3x² + 3x + 1.

3x² + 3x – 168 = 0 или, сократив на 3:

x² + x – 56 = 0.

Получили квадратное уравнение.

D = 1 – 4*1*(-56) = 225, √D = +-15.

x1 = (-1-15)/2 = -8,

x2 = (-1+15)/2 = 7.

Принимаем положительное значение х = AD = 7,

тогда CD = 7 + 1 = 8.