Question

Напиши рівняння прямої ax+by+c=0, всі точки якої розташовані на рівних відстанях від точок A(2;4) і B(6;9).

Answer 1

Напиши рівняння прямої ax+by+c=0, всі точки якої розташовані на рівних відстанях від точок A(2;4) і B(6;9).

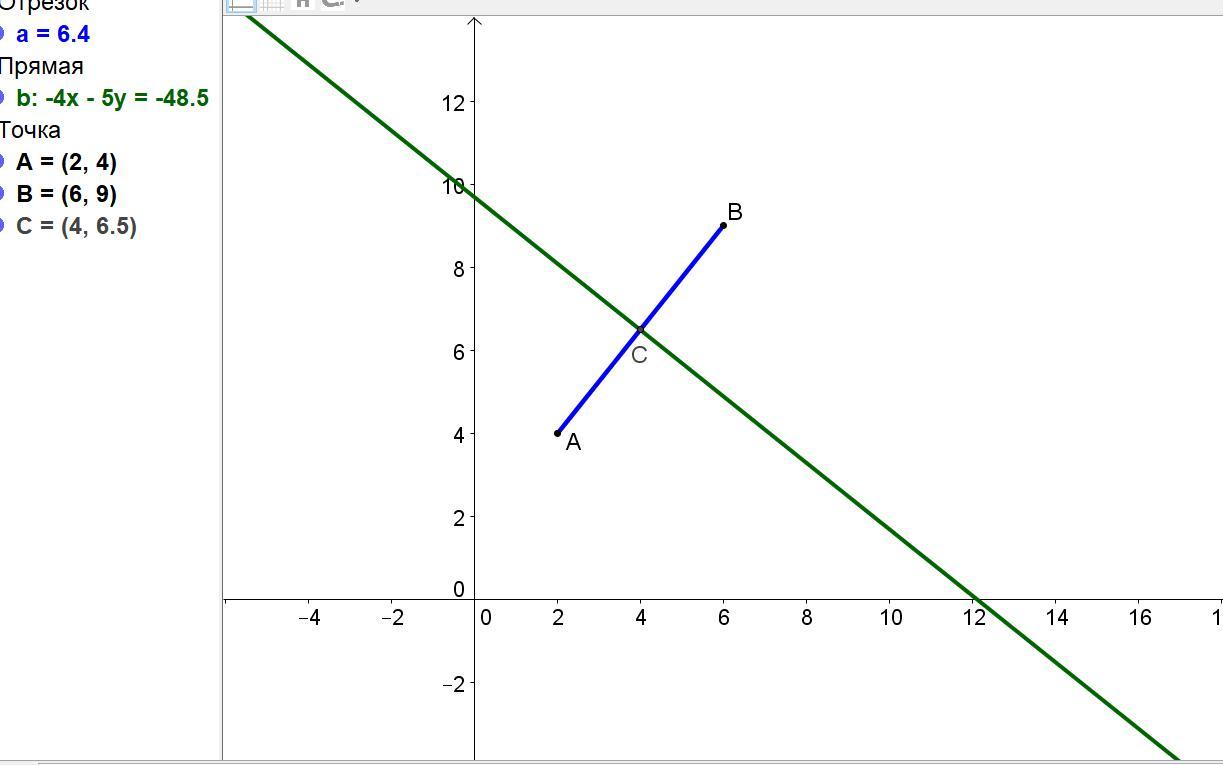
Такие точки находятся на перпендикуляре к середине  (точка С) отрезка АВ.

С = (A(2;4) + B(6;9))/2 = (4; 6,5).

Вектор АВ = (6 – 2; 9 – 4) = (4; 5).

Перпендикулярный вектор равен (5; -4).

Получаем каноническое уравнение перпендикулярной прямой по точке С и вектору:

(x – 4)/5 = (y – 6,5)/(-4).

Оно же в общем виде: -4x + 16 = 5y – 32.5  или

4x + 5y – 48,5 = 0. Можно умножить на 2, чтобы были целые коэффициенты: 8x + 10y - 97 = 0.

Если выразить уравнение относительно у, то получим уравнение с угловым коэффициентом.

y = -0,8x + 9,7.

В заданном виде ответ: : 8x + 10y - 97 = 0.